Линейных уравнений

1. Найти ранги основной и расширенной матриц системы. Если , то систем несовместна.

2. Если , то система совместна. Найти какой-либо базисный минор порядка r (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять Ir уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные In­ – r неизвестных называют свободными, и переносят в правые части уравнений.

3. Найти выражения главных неизвестных через свободные. Получено общее уравнение системы.

4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частные решения исходной системы уравнений.

Пример 4.1. Исследовать на совместность систему

Решение:

.

Таким образом, , следовательно, система несовместна.

Пример 4.2. Решить систему

Решение: . Берем два первых уравнения:

,

,

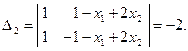
Следовательно, – общее решение. Положив, например, получим одно из частных решений: