Достаточность. Пусть . Тогда однородная система, будучи совместной, является неопределенной

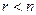Пусть . Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т.е. имеет и ненулевые решения.

Пусть дана однородная система линейных уравнений с неизвестными

Если система имеет ненулевые решения, то . Ибо при 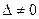система имеет единственное, нулевое решение. Если же , то ранг основной матрицы системы меньше числа неизвестных, т.е. 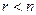. И, значит, система имеет бесконечное множество (ненулевых) решений.

Пример 4.6. Решить систему

Решение: Так как 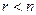, то система имеет бесчисленное множество решений. Найдем их

Стало быть – общее решение. Положив получим одно частное решение: Положив получаем второе частное решение: и т.д.

Глава II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

ВЕКТОРЫ

Основные понятия

Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.

Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина изображается с помощью вектора.

Вектор­– это направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Если А – начало вектора, а В – его конец, то вектор обозначается символом или . Вектор (у него начало в точке В, а конец в точке А) называется противоположным вектору . Вектор, противоположный вектору , обозначается .

Длиной или модулем вектора называется длина отрезка и обозначается . Вектор, дина которого равна нулю, называется нулевым вектором и обозначается 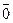. Нулевой вектор направления не имеет.

Вектор, длина которого равна единице, называется единичным вектором и обозначается через 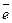. Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается .

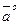Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают || .

Коллинеарные векторы могут быть направлены одинаково или противоположно.

Нулевой вектор считается коллинеарным любому вектору.

Два вектора и называются равными ( = ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства.

На рисунке 1 векторы образуют прямоугольник. Справедливо равенств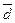о = , но . Векторы и 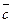– противоположные, . Равные векторы также называют свободными.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любых коллинеарны, то такие векторы компланарны.