Проекция вектора на ось. Пусть в пространстве задана ось l, т.е

Пусть в пространстве задана ось l, т.е. направленная прямая.

Проекцией точки М на ось l называется основание М₁ перпендикуляра ММ₁, опущенного из точки на ось.

Точка М₁ есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).

Если точка М лежит на оси l, то проекция точки М на ось совпадает с М.

Пусть – произвольный вектор . Обозначим через А₁ и В₁ проекции на ось l соответственно начала А и конца В вектора и рассмотрим вектор .

Проекцией вектора на ось l называется положительное число , если вектор и ось l одинаково направлены и отрицательное число , если вектор и ось l противоположно направлены (см. рис. 8). Если точки А₁ и В₁ совпадают , то проекция вектора равна нулю. Если Проекция вектора на ось l обозначается так: пр_l . Если или , то пр_l .

Угол φ между вектором и осью l (или

угол между двумя векторами) изображен на рисунке 9. Очевидно, .

Рассмотрим некоторые основные свойства проекций.

Свойство 1. Проекция вектора на ось l равна произведению модуля вектора на косинус угла φ между вектором и осью, т.е. пр­_l .

Если , то пр_l .

Если , то пр_l

(см. рис. 10).

Если , то пр_l .

Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.

Пусть, например, . Имеем пр_l­­ , т.е. пр_l пр_l + пр_l + пр_l 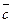(см. рис. 11).

Свойство 3. При умножении вектора на число λ его проекция на ось также умножается на это число, т.е.

пр_l .

При имеем пр_l

(свойство 1)

пр_l .

При : пр_l

пр_l .

Свойство справедливо, очевидно, и при .

Таким образом, линейные операции над

векторам приводят к соответствующим линейным операциям над проекциями этих векторов.