Свойства скалярного произведения

1. Скалярное произведение обладает переместительным свойством: .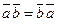

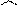
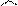
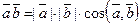, а 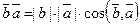. И так как , как произведение чисел и , то .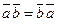

2. Скалярное произведение обладает сочетательным свойством относительно скалярного множителя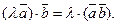

3. Скалярное произведение обладает распределительным свойством:

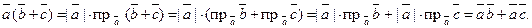
4. Скалярный квадрат вектора равен квадрату его длины: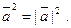

В частности: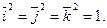

Если вектор возвести скалярно в квадрат и затем извлечь корень, то получим не первоначальный вектор, а его модуль 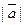, т.е.

Пример 6.1. Найти длину вектора если .

Решение:

5. Если векторы и (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е. если 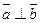, то 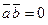. Справедливо и обратное утверждение: если 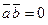и , то .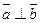

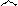
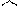
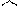Так как , то Следовательно Если же и , то 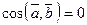. Отсюда 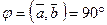, т.е. 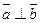. В частности:

.