Выражение скалярного произведения через координаты

Пусть заданы два вектора

и .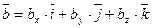

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов , , :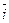

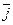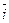
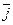
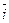
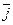
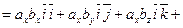
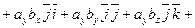
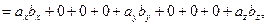
Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

Пример 6.2. Доказать, что диагонали четырехугольника, заданного координатами вершин 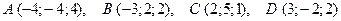, взаимно перпендикулярны.

Решение: Составим вектора и , лежащие на диагоналях данного четырехугольника. Имеем и . Найдем скалярное произведение этих векторов:

Отсюда следует, что . Диагонали четырехугольника ABCD взаимно перпендикулярны.

Некоторые приложения скалярного произведения