Определение геометрического произведения, его геометрический смысл

Рассмотрим произведение векторов , и 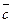, составленное следующим образом: 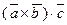. Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Выясним геометрический смысл выражения 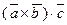. Построим параллелепипед, ребрами которого являются векторы , , 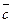и вектор (см. рис. 22).

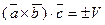Имеем: , где – площадь параллелограмма, построенного на векторах и , для правой тройки векторов и для левой, где – высота параллелепипеда. Получаем: , т.е. , где 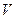– объем параллелепипеда, образованного векторами , и .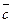

Таким образом, смешанное произведение трех векторов равно объему, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.