Поворот осей координат

Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и то же угол, а начало координат и масштаб остаются неизменными.

Пусть новая система получена поворотом системы Оху на угол α.

Пусть М – произвольная точка плоскости, – ее координаты в старой системе и – в новой системе.

Введем две полярные системы координат с общим полюсом О и полярными осям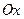и и (масштаб одинаков). Полярный радиус r в обеих системах одинаков, а полярные углы соответственно равны α + φ и φ, где φ – полярный угол в новой полярной системе.

По формулам перехода от полярных координат к прямоугольным имеем

т.е.

Но и . Поэтому

Полученные формулы называются формулами поворота осей. Они позволяют определять старые координаты произвольной точки М через новые координаты этой же точки М, и наоборот.

Если новая система координат получена из старой Оху путем параллельного переноса осей координат и последующим поворотом осей на угол α (см. рис.30), то путем введения вспомогательной системы легко получить формулы

выражающие старые координаты х и у произвольной точки через ее новые координаты и .