Условие коллинеарности векторов

Если 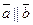, то (и наоборот), т.е.

.

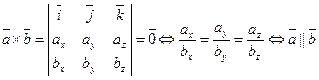Нахождение площади параллелограмма и треугольника

Согласно определению векторного произведения векторов и 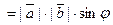, т.е. 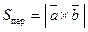. И, значит, .

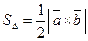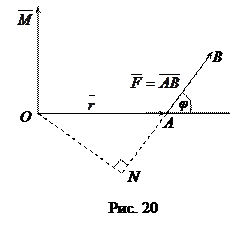Определение момента силы относительно точки

Пусть в точке А приложена сила 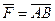и пусть О – некоторая точка пространства (см. рис.20).

Из физики известно, что моментом силы относительно точки О называется вектор 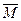, который проходит через точку О и:

1) перпендикулярен плоскости, проходящей через точки О, А, В;

2) численно равен произведению силы на плечо

;

3) образует правую тройку с векторами и .

Стало быть, .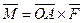

Нахождение линейной скорости вращения

Скорость 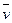точки M твердого тела, вращающегося с угловой скоростью 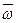вокруг неподвижной оси, определяется формулой Эйлера 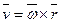, где 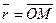, где O – некоторая точка оси (см. рис. 21).