Выражение векторного произведения через координаты

Мы будем использовать таблицу векторного произведения векторов 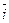, 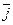и :

			-
	-
		-

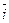
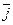
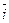
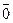
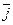
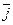
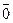
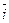
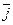
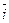
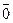
Чтобы не ошибиться со знаком, удобно пользоваться схемой:

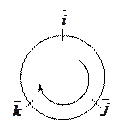если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает – третий вектор берется со знаком «минус».

Пусть заданы два вектора и 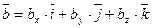. Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):

,

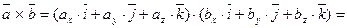
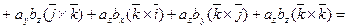
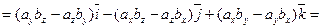
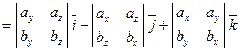т.е.

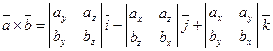. (7.1)

Полученную формулу можно записать еще короче:

(7.2)

так как правая часть равенства (7.1) соответствует разложению определителя третьего порядка по элементам первой строки. Равенство (7.2) легко запоминается.

Некоторые приложения векторного произведения