Действия над векторами, заданными проекциями

Пусть векторы и 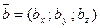заданы своими проекциями на оси координат Ox, Oy, Oz или, что то же самое

Линейные операции над векторами

Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:

1. ,

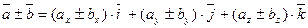или кратко 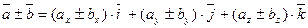. То есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).

2. 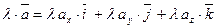или короче . То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.

Равенство векторов

Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора и 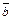равны тогда и только тогда, когда выполняются равенства: 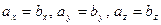, т.е.