КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Координаты вектора
Найдем координаты вектора 
, если известны координаты точек 
и 
. Имеем (см. рис.13):
.
Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала:
 |
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
И ЕГО СВОЙСТВА
Определение скалярного произведения
Скалярным произведением двух ненулевых векторов 
и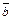 
называется число, равное произведению длин этих векторов на косинус угла между ними.
 |
Обозначается 
(или 
). Итак, по определению,
|
(6.1)
 |
где 
.
|
(см. рис. 14), а 
то получаем
(6.2)
т.е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Дата добавления: 2015-01-15; просмотров: 70; Мы поможем в написании вашей работы!; Нарушение авторских прав |