
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение взаимной ориентации векторов в пространстве
Определение взаимной ориентации векторов  ,
,  и
и 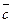 основано на следующих соображениях. Если
основано на следующих соображениях. Если 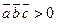 , то
, то  ,
,  ,
, 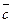 – правая тройка; если
– правая тройка; если 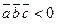 , то
, то  ,
,  ,
, 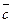 – левая тройка.
– левая тройка.
Установление компланарности векторов
Векторы  ,
,  и
и 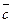 компланарны тогда и только тогда, когда их смешанное произведение равно нулю
компланарны тогда и только тогда, когда их смешанное произведение равно нулю 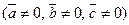 :
:
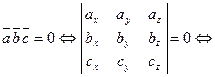 векторы
векторы  ,
,  ,
, 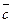 компланарны.
компланарны.
Определение объемов параллелепипеда и треугольной пирамиды
Нетрудно показать, что объем параллелепипеда, построенного на векторах  ,
,  и
и 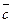 вычисляется как
вычисляется как 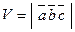 , а объем треугольной пирамиды, построенной на этих же векторах, равен
, а объем треугольной пирамиды, построенной на этих же векторах, равен 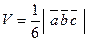 .
.

Пример 8.1. Вершинами пирамиды служат точки 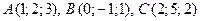 и
и 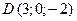 . Найти объем пирамиды.
. Найти объем пирамиды.
 Решение. Находим векторы
Решение. Находим векторы  ,
,  ,
, 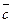 :
:
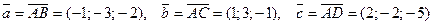 .
.
Находим 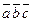 :
:
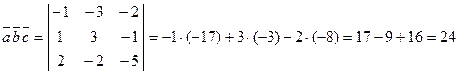 .
.
 Следовательно,
Следовательно, 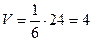 .
.
Глава III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
НА ПЛОСКОСТИ

СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ
Основные понятия
Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости. Одной из таких систем является прямоугольная(декартова) система координат.
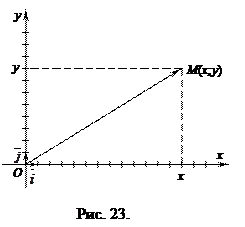 |
Прямоугольная система координат задается двумя взаимно перпендикулярными прямыми – осями, на каждой из которых выбрано положительное направление и задан единичный (масштабный) отрезок. Единицу масштаба берут обычно одинаковой для обеих осей. Эти оси называют осями координат, точку их пересечения О – началом координат. Одну из осей называют осью абсцисс (осью Оx), другую – осью ординат (осью Оy) (рис. 23).
На рисунках ось абсцисс обычно располагают горизонтально и направленной слева направо, а ось ординат − вертикально и направленной снизу вверх. Оси координат делят
плоскость на четыре области – четверти (или квадранты).
Единичные векторы осей обозначают 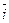 и
и 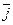
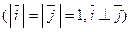 .
.
Систему координат обозначают Oxy (или 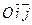 ), а плоскость, в которой расположена система координат, называют координатной плоскостью.
), а плоскость, в которой расположена система координат, называют координатной плоскостью.
Рассмотрим произвольную точку М плоскости Oxy. Вектор 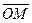 называется радиус-вектором точки М.
называется радиус-вектором точки М.
Координатами точки М в системе координат Oxy ( 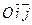 ) называются координаты радиус-вектора
) называются координаты радиус-вектора 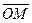 . Если
. Если 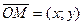 , то координаты точки М записываются так:
, то координаты точки М записываются так: 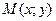 , число х называется абсциссой точки М, у – ординатой точки М.
, число х называется абсциссой точки М, у – ординатой точки М.
Эти два числа х и у полностью определяют положение точки на плоскости, а именно: каждой паре чисел х и у соответствует единственная точка М плоскости, и наоборот.
Другой практически важной системой координат является полярная система координат. Полярная система координат задается точкой О, называемой полюсом, лучом Оp,

называемой полярной осью, и единичным вектором 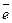 того же направления, что и луч Оp.
того же направления, что и луч Оp.
Возьмем на плоскости точку М, не совпадающую с О. Положение точки М определяется двумя числами: ее расстоянием r от полюса О и углом φ, образованным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки) (см. рис. 24).
Числа r и φ называются полярными координатами точки М, пишут 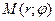 , при этом r называют полярным радиусом, φ – полярным углом.
, при этом r называют полярным радиусом, φ – полярным углом.
Для построения всех точек плоскости достаточно полярный угол φ ограничить промежутком 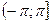 (или
(или 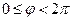 ), а полярный радиус –
), а полярный радиус – 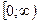 . В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, и обратно.
. В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, и обратно.
Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Оху, а полярную ось с положительной полуосью Ох. Пусть х и у – прямоугольные координаты точки М, а r и φ – ее полярные координаты.
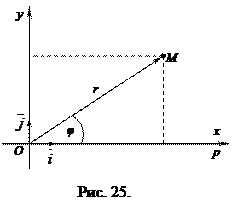 |
Из рисунка 25 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:
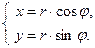
Полярные же координаты точки М выражаются через ее декартовы координаты (тот же рисунок) такими формулами:
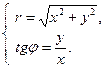
Определяя величину φ, следует установить (по знакам х и у) четверть, в которой лежит искомый угол, и учитывать, что 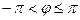 .
.

Пример 9.1. Дана точка 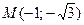 . Найти полярные координаты точки М.
. Найти полярные координаты точки М.
 Решение: Находим r и φ:
Решение: Находим r и φ:
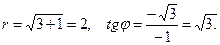
 Отсюда
Отсюда 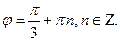 Но так как точка М лежит в 3-й четверти, то
Но так как точка М лежит в 3-й четверти, то 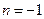 и
и 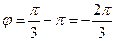 . Итак, полярные координаты точки М есть
. Итак, полярные координаты точки М есть 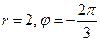 , т.е.
, т.е. 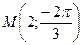 .
.
Дата добавления: 2015-01-15; просмотров: 556; Мы поможем в написании вашей работы!; Нарушение авторских прав |