
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т.е. 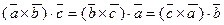 .
.
Действительно в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.
2. Смешанное произведение не меняется при перемене местами знаков векторного и смешанного умножения, т.е. 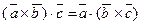 . Действительно
. Действительно 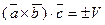 и
и 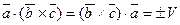 . Знак в правой части этих равенств берем одни и те же, так как тройки векторов
. Знак в правой части этих равенств берем одни и те же, так как тройки векторов  ,
,  ,
, 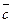 и
и  ,
, 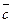 ,
,  – одной ориентации.
– одной ориентации.
Следовательно, 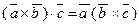 . Это позволяет записывать смешанное произведение векторов
. Это позволяет записывать смешанное произведение векторов 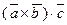 в виде
в виде 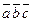 без знаков векторного и скалярного умножения.
без знаков векторного и скалярного умножения.
3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т.е. 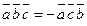 ,
, 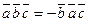 ,
, 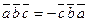 .
.
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.
4. Смешанное произведение ненулевых векторов  ,
,  и
и 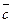 тогда и только тогда, когда они компланарны.
тогда и только тогда, когда они компланарны.
 Если
Если 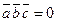 , то
, то 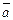 ,
,  ,
, 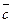 – компланарны.
– компланарны.
Допустим, что это не так. Можно было бы построить параллелепипед с объемом 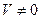 . Но так как
. Но так как 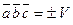 , то получили бы
, то получили бы 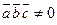 . Это противоречит условию:
. Это противоречит условию: 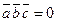 .
.
 Обратно, пусть векторы
Обратно, пусть векторы 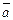 ,
,  ,
, 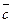 – компланарны. Тогда вектор
– компланарны. Тогда вектор 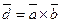 будет перпендикулярен плоскости, в которой лежат векторы
будет перпендикулярен плоскости, в которой лежат векторы 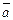 ,
,  ,
, 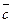 , и, следовательно
, и, следовательно  . Поэтому
. Поэтому 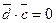 , т.е.
, т.е. 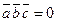 .
.
Дата добавления: 2015-01-15; просмотров: 387; Мы поможем в написании вашей работы!; Нарушение авторских прав |