Уравнение прямой, проходящей через две точки

Пусть прямая проходит через точки и . Уравнение прямой, проходящей через точку имеет вид

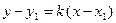, (10.6)

где k пока неизвестный коэффициент.

Так как прямая проходит через точку , то координаты этой точки должны удовлетворять уравнению (10.6): . Отсюда находим . Подставляя найденное значение k в уравнение (10.6), получим уравнение прямой, проходящей через точки и :

(10.7)

Предполагается, что в этом уравнении .

Если , то прямая, проходящая через точки и , параллельна оси ординат. Ее уравнение имеет вид .

Если , то уравнение прямой может быть записано в виде , прямая параллельна оси абсцисс.

Уравнение прямой в отрезках

т.е.

Это уравнение называется уравнением прямой в отрезках, так как числа а и b указывают, какие отрезки отсекает прямым на осях координат.