Нормальное уравнение прямой

Пусть прямая определяется заданием p и α (см. рис. 45). Рассмотрим прямоугольную систему координат Оху. Введем полярную систему, взяв О за полюс и Ох за полярную ось. Уравнение прямой можно записать в виде

т.е.

(10.11)

Уравнение (10.11) называется нормальным уравнением прямой.

Покажем, как привести уравнение (10.4) прямой к виду (10.11).

Умножим все члены уравнения (10.4) на некоторый множитель . Получим Это уравнение должно обратиться в (10.11). Следовательно, должны выполняться равенства: Из первых двух равенств находим , т.е.

Множитель 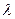называется нормирующим множителем. Согласно третьему равенству знак нормирующего множителя противоположен знаку свободного члена С общего уравнения прямой.

Пример 10.2. Привести уравнение к нормальному виду.

Решение: Находим нормирующий множитель Умножая данное уравнение на 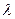, получим искомое нормальное уравнение прямой: