Каноническое уравнение эллипса

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Обозначим фокусы через и , расстояние между ними через 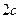, а сумму расстояний от произвольной точки эллипса до фокусов – через (см. рис. 49). По определению , т.е. .

Для вывода уравнения эллипса выберем систему координат Оху так, чтобы фокусы и лежали на оси Ох, а начало координат совпадало с серединой отрезка . Тогда фокусы будут иметь следующие координаты и .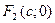

Пусть – произвольная точка эллипса. Тогда, согласно определению эллипса , т.е.

. (11.5)

Это, по сути, и есть уравнение эллипса.

Преобразуем уравнение (11.5) к более простому виду следующим образом:

,

,

,

,

.

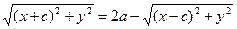Так как , то . Положим

.

(11.6)

Тогда последнее уравнение примет вид или

	.

(11.7)

Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называется каноническим уравнением эллипса.

Эллипс – кривая второго порядка.