Каноническое уравнение гиперболы

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек, этой плоскости, называемых

фокусами есть величина постоянная, меньшая, чем расстояние между фокусами.

Обозначим фокусы через и , расстояние между ними через 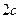, а модуль разности расстояний от каждой точки гиперболы до фокусов – через (см. рис. 49). По определению , т.е. .

Для вывода уравнения гиперболы выберем систему координат Оху так, чтобы фокусы и лежали на оси Ох, а начало координат совпадало с серединой отрезка . Тогда фокусы будут иметь

следующие координаты и .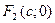

Пусть – произвольная точка гиперболы. Тогда согласно определению гиперболы или 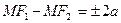, т.е. . После упрощений, как это было сделано при выводе уравнения эллипса, получим каноническое уравнение гиперболы

	,

 

(11.9)

где

	.

(11.10)

 

Гипербола есть линия второго порядка.

 

---

Поделиться:

Дата добавления: 2015-01-15; просмотров: 87; Мы поможем в написании вашей работы!; Нарушение авторских прав

---

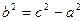⇐ Предыдущая33343536373839404142Следующая ⇒