СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Здесь А – матрица коэффициентов системы, называемая основной матрицей:

,

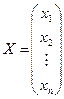– вектор-столбец из неизвестных ,

– вектор-столбец из свободных членов .

Произведение матриц 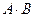определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).

Расширенной матрицей системы называется матрица системы, дополненная столбцом свободных членов

.

Решением системы называется n значений неизвестных , при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца .

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она ни имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются только над строками матрицы.

Система линейных уравнений называется однородной, если все свободные члены равны нулю:

Однородная система всегда совместна, так как является решением системы. Это решение называется нулевым или тривиальным.