Обратная матрица

Приведем доказательство для случая матрицы 3-го порядка. Пусть

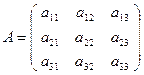, причем .

Составим союзную матрицу

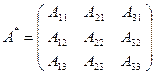
и найдем произведение матриц :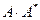

т.е.

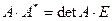(3.2)

Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2).

Аналогично убеждаемся, что

. (3.3)

Равенства (3.2) и (3.3) перепишем в виде

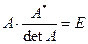и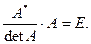

Сравнивая полученные результаты с определением (3.1), получим

т.е. .

Отметим свойства обратной матрицы:

1. ;

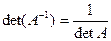2. ;

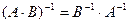3. .

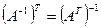Пример 3.1. Найти , если

Решение: 1) Находим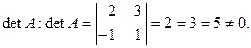

2) Находим 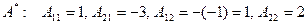, поэтому

.

3) Находим .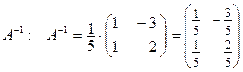

Проверка:

.

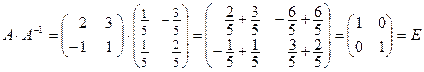Пример 3.2. Определить, при каких значениях λ существует матрица, обратная данной:

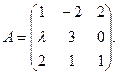
Решение: Всякая невырожденная матрицы имеет обратную. Найдем определитель матрицы А:

Если 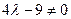, т.е. 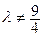, то 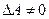, то матрица А невырожденная, имеет обратную.

Пример 3.3. Показать, что матрица А является обратной для В, если

, .

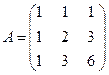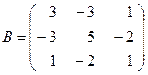Решение: Найдем произведение матриц А и В:

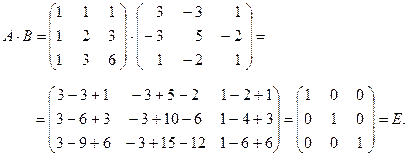
Аналогично В · А = Е. Следовательно, матрица А является обратной для В.