ОПРЕДЕЛИТЕЛИ

Основные понятия

Квадратной матрице А порядка n можно сопоставить число det A (или |A|, или Δ), называемое ее определителем следующим образом:

1. n = 1. А = ; .
2. n = 2. ; .
3. n = 3. ;

.

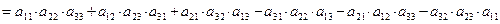Определитель матрицы А также называют его детерминантом. Правило вычисления детерминанта матрицы порядка N является довольно сложным для восприятия и применения. Однако, известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (свойство определителей 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.

Вычисление определителя 2-го порядка иллюстрируется схемой:

.

Пример 2.1. Найти определители матриц

и .

Решение:

;

.

При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:

.

Пример 2.2. Вычислить определитель матрицы

.

Решение:

.