Свойства определителей

Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.

Свойство 1 («Равноправность строк и столбцов»). Определитель не изменяется, если его строки заменить столбцами, и наоборот.

Иными словами

, .

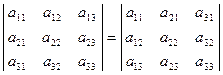В дальнейшем строки и столбцы будем просто называть рядами определителя.

Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.

Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.

Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

Действительно,

.

Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Например,

.

Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число.

Пример 2.3. Доказать, что

.

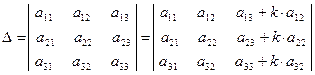Решение: Действительно, используя свойства 5, 4 и 3 получим

.

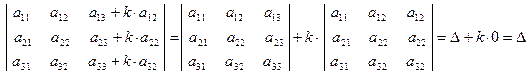Дальнейшие свойства определителя связаны с понятиями минора и алгебраического дополнения.

Минором некоторого элемента 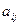определителя n-го порядка называется определитель n – 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается .

Так, если , то , .

Алгебраическим дополнением элемента 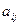определителя называется его минор, взятый со знаком «плюс», если сумма – четное число, и со знаком «минус», если эта сумма нечетная. Обозначается .

Так, , .

Свойство 7. («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-го порядка. В этом случае свойство 7 означает, что

.

В самом деле, имеем

.

Свойство 7 содержит в себе способ вычисления определителей высоких порядков.

Пример 2.4. Вычислите определитель матрицы

.

Решение: Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т.к. соответствующие им слагаемые в разложении будут равны нулю.

.

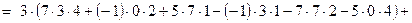
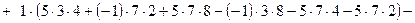
Свойство 8. Сумма произведений какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

Так, например, .