Действия над матрицами

Глава I. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

МАТРИЦЫ

Основные понятия

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или n столбцов одинаковой длины). Матрица записывается в виде

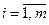или, сокращенно, , где (т.е. 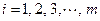) – номер строки, 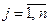(т.е. ) – номер столбца. Числа , составляющие матрицу, называются ее элементами. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.

Матрицу А называют матрицей размера m × n и пишут .

Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т.е.

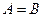, если , где , .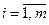

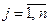Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера n × n называют матрицей n-го порядка.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.

Пример 1.1.

− единичная матрица 3-го порядка.

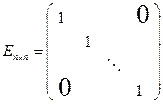
− единичная матрица n-го порядка.

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О. Имеет вид

.

В матричном исчислении матрицы О и Е играют роль чисел 0 и 1 в арифметике.

Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:

, .

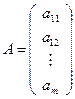Матрица размера 1 × 1, состоящая из одного числа, отождествляется с этим числом, т.е. 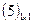есть 5.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной. Обозначается .

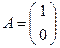Так, если , то , если , то .

Транспонированная матрица обладает следующим свойством: .

Действия над матрицами