Общее уравнение второго порядка

Рассмотрим теперь общее уравнение второй степени с двумя неизвестными:

.

Оно отличается от уравнения (11.14) наличием члена с произведением координат (В­ ≠ 0). Можно, путем поворота координатных осей на угол α, преобразовать это уравнение, чтобы в нем член с произведением координат отсутствовал.

Используя формулы поворота осей (с. 52)

, ,

выразим старые координаты через новые:

.

Выберем угол α так, чтобы коэффициент при обратился в нуль, т.е. чтобы выполнялось равенство

,

т.е.

, (11.16)

т.е.

.

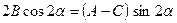Отсюда

. (11.17)

Таким образом, при повороте осей на угол α, удовлетворяющий условию (11.17), уравнение (11.15) сводится к уравнению (11.14).

Вывод: общее уравнение второго порядка (11.15) определяет на плоскости (если не считать случаев вырождения или распадения) следующие кривые: окружность, эллипс, гиперболу, параболу.

Замечание: Если А = С, то уравнение (11.17) теряет смысл. В этом случае 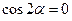(см. (11.16)), тогда , т.е. . Итак, при А = С систему координат следует повернуть на .