Уравнение сферы

Найдем уравнение сферы радиуса R с центром в точке 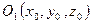. Согласно определению сферы расстояние любой ее точки 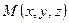от центра 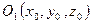равен радиусу R, т.е. 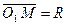. Но , где . Следовательно,

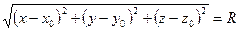
или

Это и есть искомое уравнение сферы. Ему удовлетворяют координаты любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.

Если центр сферы совпадает с началом координат, то уравнение сферы принимает вид

Если же дано уравнение , то оно, вообще говоря, определяет в пространстве некоторую поверхность.

Выражение «вообще говоря» означает, что в отдельных случаях уравнение может определять не поверхность, а точку, линию, или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».

Так, уравнению 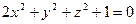не удовлетворяют никакие действительные значения x, y и z. Уравнению удовлетворяют лишь координаты точек, лежащих на оси Ox (из уравнения следует: , а х – любое число)

Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач:

1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.
2. Дано уравнение . Исследовать форму поверхности, определяемой этим уравнением.