
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Исследование форм параболы по ее уравнению
1. В уравнении (11.13) переменная  входит в четной степени, значит, парабола симметрична относительно оси
входит в четной степени, значит, парабола симметрична относительно оси 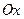 ; ось
; ось 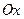 является осью симметрии параболы.
является осью симметрии параболы.
2. Так как  , то из (11.13) следует, что
, то из (11.13) следует, что  . Следовательно, парабола расположена справа от оси
. Следовательно, парабола расположена справа от оси  .
.
3. При  имеем
имеем  , следовательно, парабола проходит через начало координат.
, следовательно, парабола проходит через начало координат.
4. При неограниченном возрастании x модуль y также неограниченно возрастает.
Парабола  имеет вид (форму), изображенный на рисунке 61. Точка
имеет вид (форму), изображенный на рисунке 61. Точка  называется вершиной параболы, отрезок
называется вершиной параболы, отрезок  называется фокальным радиусом точки M.
называется фокальным радиусом точки M.
 |
|
 ,
,  ,
, 
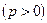 также определяют параболы, они изображены на рисунке 62.
также определяют параболы, они изображены на рисунке 62.

Нетрудно показать, что график квадратного трехчлена  , где
, где  , В и С любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.
, В и С любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.
Общее уравнение линий второго порядка
Дата добавления: 2015-01-15; просмотров: 266; Мы поможем в написании вашей работы!; Нарушение авторских прав |