Уравнение линии в пространстве

Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, общих двум поверхностям.

Если и – уравнения двух поверхностей, определяющих линию L то, координаты этой линии удовлетворяют системе двух уравнений с тремя неизвестными:

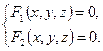(12.1)

Уравнения системы (12.1) называются уравнениями линии в пространстве. Например, 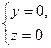есть уравнения оси Ox.

Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 67). В этом случае ее задают векторным уравнением

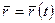(12.2)

или параметрическими уравнениями

проекций вектора (12.2) на оси координат.

Например, параметрические уравнения винтовой линии имеют вид

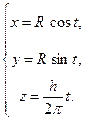
Если точка M равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка M описывает винтовую линию (см. рис. 68).