Непрерывность несобственного интеграла по параметру

Радиус сходимости степенного ряда. Формула Коши-Адамара

Круг сходимости степенного ряда — это круг вида

, ,

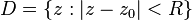в котором ряд абсолютно сходится, а вне его, при , расходится. Иными словами, круг сходимости степенного ряда есть внутренность множества точек сходимости ряда. Круг сходимости может вырождаться в пустое множество, когда , и может совпадать со всей плоскостью переменного , когда .

Радиус сходимости[править | править вики-текст]

Радиус круга сходимости называется радиусом сходимости ряда.

Радиус сходимости ряда Тейлора аналитической функции равен расстоянию от центра ряда до множества особых точек функции, и может быть вычислен по формуле Коши — Адамара:

Эта формула выводится на основе признака Коши.