
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Степенные ряды. Первая теорема Абеля
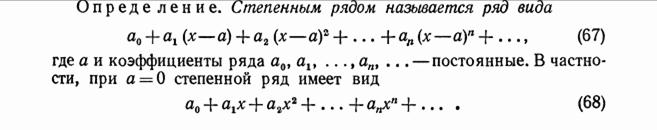
Т: Пусть  — степенной ряд с комплексными коэффициентами и радиусом сходимости
— степенной ряд с комплексными коэффициентами и радиусом сходимости 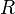 .
.
Если ряд  является сходящимся, тогда:
является сходящимся, тогда:
 .
.
Доказательство
Заменой переменных  , можно считать
, можно считать  . Также (необходимым подбором
. Также (необходимым подбором  ) можно предположить
) можно предположить  . Обозначим
. Обозначим  частичные суммы ряда
частичные суммы ряда  . Согласно предположению
. Согласно предположению 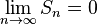 и нужно доказать, что
и нужно доказать, что 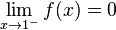 .
.
Рассмотрим  . Тогда (приняв
. Тогда (приняв 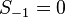 ):
):

Отсюда получается 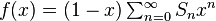 .
.
Для произвольного  существует натуральное число
существует натуральное число  , что
, что  для всех
для всех 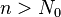 , поэтому:
, поэтому:

Правая часть стремится к  когда
когда  стремится к 1, в частности она меньше
стремится к 1, в частности она меньше 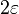 при следовании
при следовании  к 1.
к 1.
Необходимое условие экстремума

Признак сравнения рядов в предельной форме
Если 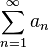 и
и  есть строго положительные ряды и
есть строго положительные ряды и
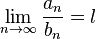 ,
,
то при  из сходимости
из сходимости  следует сходимость
следует сходимость 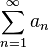 , а при
, а при  из расходимости
из расходимости  следует расходимость
следует расходимость 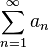 .
.
Дата добавления: 2015-01-19; просмотров: 246; Мы поможем в написании вашей работы!; Нарушение авторских прав |