Дифференциал функции двух переменных

Пусть функция z = f(x,y), имеет в точке М₀(х₀,у₀) частные производные f ^/_x (х₀,у₀) и f ^/_у (х₀,у₀).

О. Полным приращением функции z = f(x,y) в точке М₀(х₀,у₀) называется разность

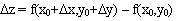
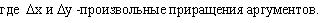
Пусть приращение функции z =f(x,y) можно представить в виде

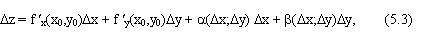
где , то функция называется дифференцируемой в точке M ₀ (х₀,у₀).

О. Полным дифференциалом функции z=f(x,y) называется главная часть полного приращения 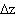, линейная относительно приращений её аргументов 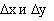. Полный дифференциал функции (если он существует) равен сумме всех ее частных дифференциалов и вычисляется по формуле:

При достаточно малых (по абсолютному значению) приращениях аргументов, полное приращение функции можно с как угодно малой относительной погрешностью заменить ее полным дифференциалом. Дифференциалы dх и dy независимых аргументов функции х и у совпадают с их приращениями соответственно . Таким образом,

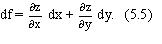
6. Числовой ряд. Сумма ряда. Необходимый признак сходимости.

Числовым рядом называется сумма вида

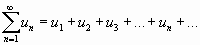, (1.1)

где , , ,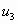…, ,…, 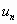называемые членами ряда, образуют бесконечную последовательность; член 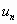называется общим членом ряда.

Суммы

…………..

,

составленные из первых членов ряда (1.1), называются частичными суммами этого ряда.

Каждому ряду можно сопоставить последовательность частичных сумм .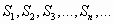

Если при бесконечном возрастании номера n частичная сумма ряда стремится к пределу 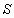, то ряд называется сходящимся, а число 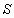- суммой сходящегося ряда, т.е.

и .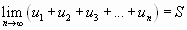

Эта запись равносильна записи

.

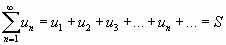Если частичная сумма ряда (1.1) при неограниченном возрастании n не имеет конечного предела (стремится к 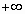или 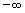), то такой ряд называется расходящимся.

Если ряд сходящийся, то значение при достаточно большом n является приближенным выражением суммы ряда S.

Разность 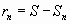называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е. 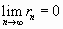, и наоборот, если остаток стремится к нулю, то ряд сходится.