
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры. сходится, так как выполняется условие предельной формы радикального признака теоремы Коши
1. Ряд

сходится, так как выполняется условие предельной формы радикального признака теоремы Коши
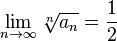
2. Рассмотрим ряд
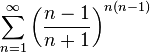
 ряд сходится.
ряд сходится.
3. Признак сравнения положительных рядов в конечной форме
Пусть даны два знакоположительных ряда:
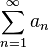 и и  Тогда, если, начиная с некоторого места (
Тогда, если, начиная с некоторого места ( 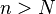 ), выполняется неравенство: ), выполняется неравенство:
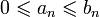 ,
то из сходимости ряда ,
то из сходимости ряда  следует сходимость следует сходимость 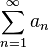 .
Или же, если ряд .
Или же, если ряд 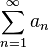 расходится, то расходится и расходится, то расходится и  . .
|
Доказательство
Обозначим  частные суммы ряда
частные суммы ряда 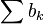 . Из неравенств
. Из неравенств 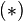 следует, что
следует, что 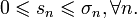 Поэтому из ограниченности
Поэтому из ограниченности 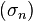 вытекает ограниченность
вытекает ограниченность  а из неограниченности
а из неограниченности  следует неограниченность
следует неограниченность  Справедливость признака вытекает из критерия сходимости для
Справедливость признака вытекает из критерия сходимости для 
4. Разложение в ряд Тейлора функций sin x, cos x


5. Дифференциал. Геометрический смысл дифференциала. Касательная плоскость.
Дата добавления: 2015-01-19; просмотров: 283; Мы поможем в написании вашей работы!; Нарушение авторских прав |