Доказательство

Рассмотрим функцию , где число выберем таким, чтобы выполнялось равенство , которое равносильно следующему:
.

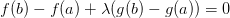Заметим, что 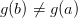, так как в противном случае согласно Теореме Роллясуществовала бы точка такая, что вопреки условиям данной теоремы. Из равенства 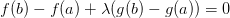следует, что .

Так как функция при любом непрерывна на отрезке 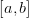и дифференцируема на интервале , а при значении , определяемом предыдущей формулой, принимает равные значения в точках и , то по теореме Ролля существует точка такая, что 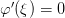, т.е. 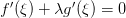, откуда 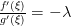. Из этого равенства и формулы следует .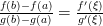

1. Замечание. Теорема Лагранжа — частный случай теоремы Коши .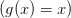

2. Замечание. Теорему Коши нельзя получить используя теорему Лагранжа отдельно к числителю и к знаменателю.

16. Равномерная сходимость несобственного интеграла

17. Признак Вейерштрасса равномерной сходимости несобственного интеграла

18. Дифференцируемость функции f. Дифференцируемость и частные производные

19. ТЕОРЕМА 3 КРИТЕРИЙ РАЗЛОЖЕНИЯ ФУНКЦИИ В СТЕПЕННОЙ РЯД
Для того, чтобы бесконечно дифференцируемая в окрестности точки функция f (x) разлагалась в ряд Тейлора в окрестности этой точки, необходимо и достаточно, чтобы

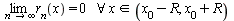
ДОКАЗАТЕЛЬСТВО

Если ряд Тейлора сходится к S(x) ≠ f (x) , то из равенств

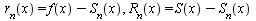
следует, что .

Если же S(x) = f (x), то, очевидно, .

ТЕОРЕМА 4 ДОСТАТОЧНОЕ УСЛОВИЕ РАЗЛОЖЕНИЯ ФУНКЦИИ В СТЕПЕННОЙ РЯД
Если функция f и все её производные ограничены в совокупности на интервале , т.е. существует такая постоянная M > 0, что для всех 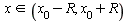и всех n=0,1,2,… выполняется неравенство
,

то функция f представляется рядом Тейлора (10), сходящимся в каждой точке интервала .