
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Признак Вейерштрасса
Рассмотрим ряд: 
Пусть существует последовательность  такая, что для любого
такая, что для любого 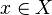 выполняется неравенство
выполняется неравенство  , кроме того, ряд
, кроме того, ряд  сходится. Тогда ряд
сходится. Тогда ряд  сходится на множестве
сходится на множестве 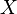 абсолютно и равномерно.
абсолютно и равномерно.
Для доказательства достаточно проверить справедливость критерия Коши.
14. Гамма-функция. Элементарные свойства
Если вещественная часть комплексного числа  положительна, то Гамма-функция определяется через абсолютно сходящийся интеграл
положительна, то Гамма-функция определяется через абсолютно сходящийся интеграл
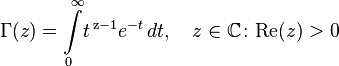
Основное свойство гамма-функции это её рекуррентное уравнение

которое, при фиксированном начальном условии, единственным образом определяет логарифмически выпуклое решение, то есть саму гамма-функцию. Теорема о единственности.
Для Г-функции справедлива формула дополнения Эйлера:
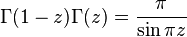 .
.
И формула умножения Гаусса:

Частный случай которой при n=2 был получен Лежандром:

Гамма-функция не имеет нулей на всей комплексной плоскости.  является мероморфной на комплексной плоскости и имеющей простые полюса в точках
является мероморфной на комплексной плоскости и имеющей простые полюса в точках  Гамма-функция имеет полюс первого порядка в
Гамма-функция имеет полюс первого порядка в  для любого натурального
для любого натурального  и нуля; вычет в этой точке задается так
и нуля; вычет в этой точке задается так
 .
.
Основное, но полезное свойство, которое может быть получено из предельного определения:
 .
.
Гамма-функция дифференцируема бесконечное число раз, и  , где
, где  часто называют «пси-функцией», или дигамма-функцией. Гамма-функция и бета-функция связаны следующим соотношением:
часто называют «пси-функцией», или дигамма-функцией. Гамма-функция и бета-функция связаны следующим соотношением:
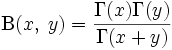 .
.


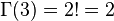
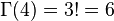

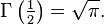
15. Обобщения формулы Лагранжа. (Теорема Коши)
Если функции  и
и 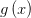 непрерывны на отрезке
непрерывны на отрезке 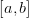 , дифференцируемы на интервале (a,b), причем
, дифференцируемы на интервале (a,b), причем 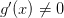 во всех точках этого интервала, то найдется хотя бы одна точка
во всех точках этого интервала, то найдется хотя бы одна точка  такая, что
такая, что 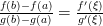 .
.
Дата добавления: 2015-01-19; просмотров: 264; Мы поможем в написании вашей работы!; Нарушение авторских прав |