
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критерий Коши равномерной сходимости
| Теорема (Критерий Коши равномерной сходимости): |
Ряд равномерно сходится на 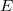 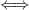 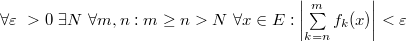
|
| Доказательство: |

|
 Пусть ряд равномерно сходится. Пусть ряд равномерно сходится.

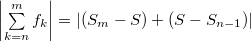 , где , где  — сумма ряда. Тогда — сумма ряда. Тогда
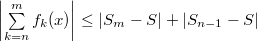 По определению равномерной сходимости,
По определению равномерной сходимости, 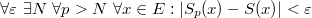 . .
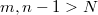 В силу предыдущего неравенства,
В силу предыдущего неравенства,  , то есть, выполняется условие критерия Коши. , то есть, выполняется условие критерия Коши.
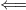 Пусть выполняется условие критерия Коши. Пусть выполняется условие критерия Коши.
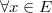 для для  выполняется критерий Коши сходимости числовых рядов. Значит, этот ряд сходится. На всем выполняется критерий Коши сходимости числовых рядов. Значит, этот ряд сходится. На всем 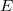 определена его сумма. Осталось установить равномерную сходимость ряда.
По условию критерия Коши, определена его сумма. Осталось установить равномерную сходимость ряда.
По условию критерия Коши, 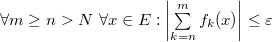 Как и в первой половине доказательства,
Как и в первой половине доказательства,  , но , но  . В неравенстве с . В неравенстве с  можно подставлять любой фиксированный можно подставлять любой фиксированный  . Устремим . Устремим 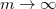 : :  Значит, определение равномерной сходимости проверено.
Значит, определение равномерной сходимости проверено.
|

|
[править]Признак Вейерштрасса
Существует простой признак для проверки равномерной сходимости (признак Вейерштрасса)
Можно рассматривать  и при этом сохраняется терминология числовых рядов, связанная с абсолютной и условной сходимостью.
и при этом сохраняется терминология числовых рядов, связанная с абсолютной и условной сходимостью.
Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость.
| Теорема (Вейерштрасс): |
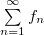 , ,  , ,  , , 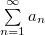 — сходится. Тогда — сходится. Тогда 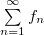 равномерно сходится на равномерно сходится на 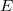 . .
|
| Доказательство: |

|
Применим критерий Коши:
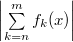  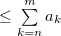
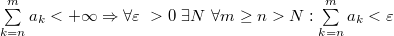 Сопоставляя с предыдущим неравенством, которое верно
Сопоставляя с предыдущим неравенством, которое верно 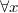 , ,
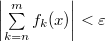 . Тогда, по критерию Коши, ряд равномерно сходится. . Тогда, по критерию Коши, ряд равномерно сходится.
|

|
[править]Признак Абеля-Дирихле
| Теорема (Абель-Дирихле): |
Для равномерной сходимости на множестве 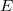 ряда ряда 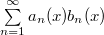 , , 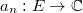 и и  достаточно, чтобы выполнялась пара условий достаточно, чтобы выполнялась пара условий 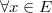 :
1)Частичные суммы :
1)Частичные суммы 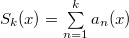 ряда ряда 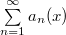 равномерно ограничены на равномерно ограничены на 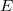 ;
2)Последовательность функций ;
2)Последовательность функций  монотонна и сходится к нулю на монотонна и сходится к нулю на 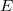 . .
|
| Доказательство: |

|
Монотонность последовательности  позволяет при каждом позволяет при каждом 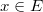 записать оценку: записать оценку:
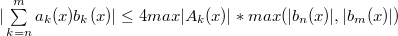 где
где 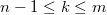 и в качестве и в качестве  возьмем возьмем 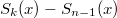 .
Если выполнена пара условий 1) и 2), то с одной стороны существует такая постоянная .
Если выполнена пара условий 1) и 2), то с одной стороны существует такая постоянная 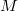 ,что ,что 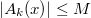 при любом при любом 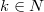 и любом и любом 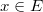 , а с другой стороны, какого бы ни было число , а с другой стороны, какого бы ни было число 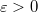 , при всех достаточно больших значениях , при всех достаточно больших значениях 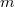 и и 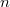 и любом и любом 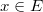 будет выполнено неравенство будет выполнено неравенство  . Значит, что при всех достаточно больших значениях . Значит, что при всех достаточно больших значениях 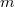 и и 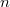 и любом и любом 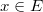 будет будет 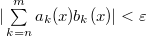 , т.е. для рассматриваемого ряда выполнен критерий Коши равномерной сходимости. , т.е. для рассматриваемого ряда выполнен критерий Коши равномерной сходимости.
|

|
Теорема о непрерывности суммы функционального ряда.
Теорема. Если все члены ряда  (1) - непрерывные на [a;b] ф-ции, а ряд (1) сх-ся равномерно на [a;b], то его сумма S(x) также непрерывна на отрезке [a;b].
(1) - непрерывные на [a;b] ф-ции, а ряд (1) сх-ся равномерно на [a;b], то его сумма S(x) также непрерывна на отрезке [a;b].
Док-во: Пусть  - произв.точка [a;b]. Для опр-ности будем считать, что
- произв.точка [a;b]. Для опр-ности будем считать, что 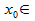 (a;b). Нужно док-ть, что S(x)=
(a;b). Нужно док-ть, что S(x)=  непрерывна в
непрерывна в  , т.е
, т.е 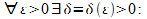
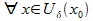

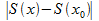 <
<  (2),
(2), 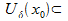 [a;b]. По усл-ю, ряд (1) равномерно сх-ся на [a;b], т.е
[a;b]. По усл-ю, ряд (1) равномерно сх-ся на [a;b], т.е 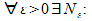
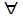 n
n 
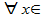 [a;b]
[a;b] 
 <
< 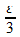 (3), где
(3), где 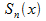 =
=  .Фиксируем номер
.Фиксируем номер 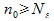 , тогда при n=
, тогда при n= 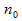 из (3) получаем:
из (3) получаем: 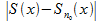 <
< 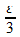 (4). В частности, при x=
(4). В частности, при x= 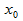 находим
находим 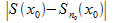 <
< 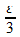 (5). Ф-ция
(5). Ф-ция  (x) непрерывна в
(x) непрерывна в  как сумма конечного числа непрерывных ф-ций. По опр-ю непрерывности
как сумма конечного числа непрерывных ф-ций. По опр-ю непрерывности 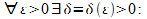
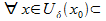 [a;b]
[a;b] 
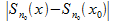 <
< 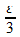 (6). Восп. рав-вом S(x)-S(
(6). Восп. рав-вом S(x)-S( 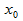 )=(S(x)-
)=(S(x)-  (x))+(
(x))+( 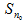 (x)-
(x)-  (
(  ))+(
))+(  (
( 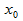 )-S(
)-S( 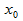 )). Отсюда получаем, исп. (4)-(6) и нер-во треугольника :
)). Отсюда получаем, исп. (4)-(6) и нер-во треугольника : 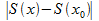 <
<  , для
, для 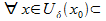 [a;b], т.е справедливо утв-е (2). В силу произвольности точки
[a;b], т.е справедливо утв-е (2). В силу произвольности точки  ф-ция S(x) непрерывна на отрезке [a;b].
ф-ция S(x) непрерывна на отрезке [a;b].
2. Радикальный признак Коши (сходимости числового ряда):
Если для числового ряда
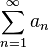 с неотрицательными членами существует такое число
с неотрицательными членами существует такое число 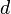 , ,  , что, начиная с некоторого номера, выполняется неравенство , что, начиная с некоторого номера, выполняется неравенство  , то данный ряд сходится. , то данный ряд сходится.
|
Дата добавления: 2015-01-19; просмотров: 377; Мы поможем в написании вашей работы!; Нарушение авторских прав |