
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доказательство.
Рассмотрим две последовательности частичных сумм ряда  и
и  .
.
Первая последовательность убывает:  по первому условию.
по первому условию.
По тому же условию вторая последовательность возрастает: 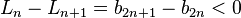 .
.
Первая последовательность мажорирует вторую, а именно, для любых 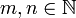 имеет место неравенство
имеет место неравенство
 ,
, поэтому они обе сходятся как монотонные ограниченные последовательности.
Осталось заметить, что  , поэтому они сходятся к общему пределу
, поэтому они сходятся к общему пределу  , который и является суммой исходного ряда.
, который и является суммой исходного ряда.
Попутно мы показали, что для любой частичной суммы ряда  имеет место оценка
имеет место оценка  .
.
10. Интеграл с параметром. Непрерывность
Пусть в двумерном евклидовом пространстве задана область  , на которой определена функция
, на которой определена функция  двух переменных.
двух переменных.
Пусть далее,  .
.
Функция  и называется интегралом, зависящим от параметра.
и называется интегралом, зависящим от параметра.
Пусть функция  непрерывна в области
непрерывна в области 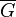 как функция двух переменных. Тогда функция
как функция двух переменных. Тогда функция  непрерывна на отрезке
непрерывна на отрезке  .
.
Доказательство[скрыть]
Рассмотрим приращение интеграла, зависящего от параметра. 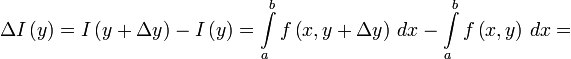
 .
.
По теореме Кантора, непрерывная на компакте функция равномерно непрерывна на нём, то есть 
 .
.
Следовательно, 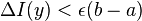 при
при  , что и означает непрерывность функции
, что и означает непрерывность функции
11. бета-функцией (  -функцией, бета-функцией Эйлера или интегралом Эйлера I рода) называется следующая специальная функция от двух переменных:
-функцией, бета-функцией Эйлера или интегралом Эйлера I рода) называется следующая специальная функция от двух переменных:
 ,
,
определённая при 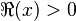 ,
,  .
.
Дата добавления: 2015-01-19; просмотров: 224; Мы поможем в написании вашей работы!; Нарушение авторских прав |