КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Окружность. Уравнение окружности.
Простейшей кривой второго порядка является окружность. Напомним, что окружностью радиуса R с центром в точке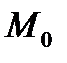 
называется множество всех точек М плоскости, удовлетворяющих условию 
. Пусть точка М в прямоугольной системе координат Оху имеет координаты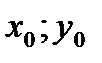 
, а 
– произвольная точка окружности (см. рис. 48).
| О |
| х |
| у |
| R |
|
|
| Рис. 48. |
Тогда из уравнения получим уравнение
|
(11.2)
Уравнению (11.2) удовлетворяют координаты любой точки данной окружности и не удовлетворяют координаты никакой точки, не лежащих на окружности.
Уравнение (11.2) называется каноническим уравнением окружности.
В частности, полагая 
и 
, получим уравнение окружности с центром в начале координат 
Уравнение окружности (11.2) после несложных преобразований примет вид 
При сравнении этого уравнения с общим уравнением (11.1) кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия:
1) коэффициенты при 
и 
равны между собой;
2) отсутствует член, содержащий произведение 
текущих координат
Рассмотрим обратную задачу. Положив в уравнении (11.1) значения 
и 
получим
(11.3)
Преобразуем это уравнение:
т.е.
т.е.
(11.4)
Отсюда следует, что уравнение (11.3) определяет окружность при условии, 
Ее центр находится в точке 
, а радиус 
. Если же 
, то уравнение (11.3) имеет вид 
. Ему удовлетворяют координаты единственной точки . В этом случае говорят: «окружность выродилась в точку» (имеет нулевой радиус).
Если 
, то уравнение (11.4) а, следовательно, и равносильное уравнение (11.3) не определяет никакой линии, так как правая часть уравнения (11.4) отрицательна, а левая часть – не отрицательна (говорят: «окружность мнимая»).
34.Эллипс ( вершины, оси, полуоси, фокусы…).Уравнение эллипса.
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
| О |
|
|
|
| х |
| у |
| Рис. 49. |
и 
, расстояние между ними через 
, а сумму расстояний от произвольной точки эллипса до фокусов – через 
(см. рис. 49). По определению 
, т.е. 
.
Для вывода уравнения эллипса выберем систему координат Оху так, чтобы фокусы и лежали на оси Ох, а начало координат совпадало с серединой отрезка 
. Тогда фокусы будут иметь следующие координаты и .
Пусть – произвольная точка эллипса. Тогда, согласно определению эллипса 
, т.е.
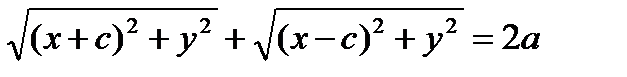. (11.5)
Это, по сути, и есть уравнение эллипса.
Преобразуем уравнение (11.5) к более простому виду следующим образом:
,
,
,
,
.
 .
|
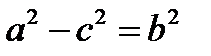, то 
. Положим
(11.6)
 .
|
или
(11.7)
Можно доказать, что уравнение (11.7) равносильно исходному уравнению. Оно называется каноническим уравнением эллипса.
Эллипс – кривая второго порядка.
Дата добавления: 2015-01-19; просмотров: 24; Нарушение авторских прав