Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей.

Угол между двумя плоскостями

Угол между двумя плоскостями равен углу между их нормальными векторами. Пусть две пересекающиеся плоскости A₁x + B₁y + C₁z + D₁ = 0 и A₂y + B₂y + C₂z + D₂ = 0 имеют нормальные векторы =(A₁;B₁; C₁) и 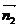=(A₂; B₂; C₂). Тогда угол между этими плоскостями вычисляется по формуле:

Условие параллельности и перпендикулярности двух плоскостей

Для того чтобы две плоскости были параллельны, их нормальные векторы и 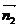должны быть коллинеарны, т.е. , где λ≠0. Если ни одна из координат векторов и 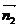не равна нулю, то из последнего равенства следует, что:

A₁ / A₂ = B₁ / B₂ = C₁ / C₂,

т.е. коэффициенты при соответствующих координатах пропорциональны.

Для того чтобы плоскости были перпендикулярны, их нормальные векторы и 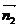также должны быть перпендикулярны, т.е. их скалярное произведение равно нулю: . Отсюда следует, что:

A₁A₂ + B₁B₂ + C₁C₂ = 0.