КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Перпендикулярно данному вектору.
|
|
|
| х |
| у |
| z |
| O |
|
| Рис. 69. |
плоскость Q задана точкой 
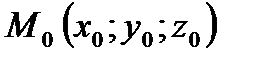и вектором 
, перпендикулярным этой плоскости (см. рис. 69). Выведем уравнение плоскости Q. Возьмем на ней произвольную точку 
и составим вектор
.
При любом расположении точки М на плоскости Q векторы 
и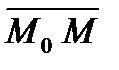 
взаимно перпендикулярны, поэтому их скалярное произведение равно нулю: 
, т.е.
(12.3.)
Координаты любой точки плоскости Q удовлетворяют уравнению (12.3), координаты точек, не лежащих на плоскости Q , этому уравнению не удовлетворяют (для них 
).
Уравнение (12.3) называется уравнением плоскости, проходящей через данную точку 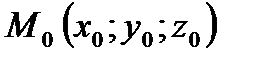перпендикулярно вектору . Оно первой степени относительно текущих координат x, y и z. Вектор называется нормальным вектором плоскости.
Придавая коэффициентам А, В и С уравнения (12.3) различные значения, можно получить уравнение любой плоскости, проходящей через точку 
. Совокупность плоскостей, проходящих через данную точку называется связкой плоскостей, а уравнение (12.3) – уравнением связки плоскостей.
Дата добавления: 2015-01-19; просмотров: 227; Мы поможем в написании вашей работы!; Нарушение авторских прав |