Необходимый признак сходимости ряда.

Ответ:Теорема: Пусть числовой ряд: u₁+u₂+...+u_n+... , (1) сходится, а S - его сумма. Тогда при неограниченном возрастании числа n членов ряда его общий член u_n стремится к нулю. Доказательство. Из условия теоремы имеем: , 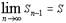. Так как S_n - S_n-1 = u_n то . Следует отметить, что этот признак является лишь необходимым, но не достаточным признаком сходимости ряда, так как можно указать ряд, для которого выполняется равенство а он, однако не является сходящимся. Так гармонический ряд: для которого 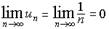расходится. Но согласно доказанному необходимому признаку сходимости ряда, если: ,то ряд (1) расходится. В самом деле, если бы он сходился, то 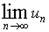равнялся бы нулю. Таким образом, доказанная нами теорема иногда позволяет, не вычисляя суммы S_n, сделать заключение о расходимости того или иного ряда. Например, ряд: 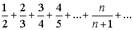расходится, так как: .