Двойной интеграл, как предел интегральной суммы.

Ответ:Пусть дана функция: Z=f(x,y), которая определена – в некоторой области 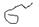, плоскости xOy (смотри рис. 1) т.е. в 13 вопросе – Задачи приводящие к понятию “двойного интеграла”. Разобьём область 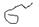- на n мелких участков , на каждом из которых – выберем точку (x_i, y_i). 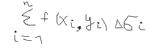- сумма называется – интегральной суммой – от функции f(x,y) по области 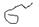. 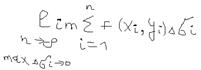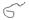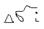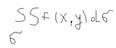Если существует конечный предел – последовательности интегральных сумм: При неограниченном возрастании числа n – участков , так что каждый из них – стягивается в точку (x_i,y_i) – независящий от способа разбиения области - на участке , и от выбора точек (x_i,y_i) – на этих участках, то этот предел – называется – двойным интегралом – от функции f(x,y) – по области , и обозначается так: , так по определению: 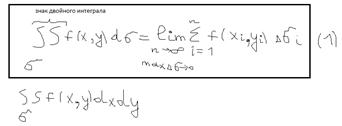С учётом определения (1) - объём цилиндрического тела равен: 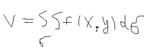. Масса неоднородной пластинки: 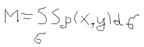. Теорема: Двойной интеграл - от функции f(x,y) – непрерывной в ограниченной - замкнутой области - существует.