Интервал сходимости, радиус сходимости степенного ряда.

Ответ:Сформулируем понятия области и интервала сходимости ряда, укажем способ определения радиуса сходимости, на примере обозначим специфику нахождения радиуса и интервала сходимости ряда, запишем гармонический расходящийся ряд и знакочередующийся ряд, сходящийся условно. В соответствии с теоремой Абеля отметим: при условии, что x₁ является точкой сходимости ряда (30.2) ряд предполагает сходимость абсолютно во всех точках интервала 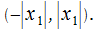Если 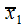есть точка расходимости (30.2), то во всех точках интервалов 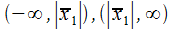ряд расходится. Тогда заключим: имеется такое число R, что на 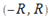ряд (30.2) сходится абсолютно, а на 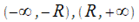расходится. В этом случае справедлива ниже обозначенная теорема. Т: Область сходимости ряда (30.2) — это интервал 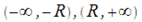предполагается расходимость ряда. Интервал R определен в качестве его радиуса сходимости. Существуют некоторые ряды, для которых интервал сходимости вырождается в точку (R=0) , при этом, имеются и такие ряды, для которых интервал охватывает всю ось 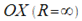. Если x=R , то ряд может расходиться и сходиться. Это зависит от конкретного ряда. Запишем способ нахождения радиуса сходимости ряда (30.2). Исследуем ряд, составленный их абсолютных величин его членов 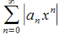и используем по отношению к нему признак Даламбера: 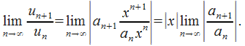При условии, что 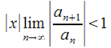(иначе выражаясь, 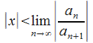) ряд из абсолютных величин членов (30.2) сходится и ряд (30.2) сходится абсолютно. Запишем: 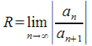(30.4). Если 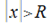, то ряд (30.2) расходится, поскольку общий член ряда 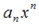не стремится к 0. Получается, что формула (30.4) обеспечивает радиус сходимости.