
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ряды Тейлора и Маклорена.
Ответ:Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора: 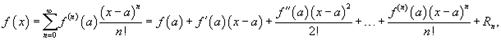 где Rn − остаточный член в форме Лагранжа определяется выражением
где Rn − остаточный член в форме Лагранжа определяется выражением 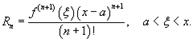 Если приведенное разложение сходится в некотором интервале x, т.е.
Если приведенное разложение сходится в некотором интервале x, т.е.  , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a. Если a = 0, то такое разложение называется рядом Маклорена:
, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a. Если a = 0, то такое разложение называется рядом Маклорена: 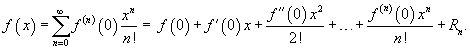 Разложение некоторых функций в ряд Маклорена: 1)
Разложение некоторых функций в ряд Маклорена: 1) 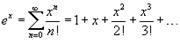 ; 2)
; 2) 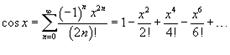 ; 3)
; 3) 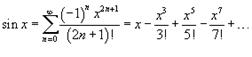 ; 4)
; 4) 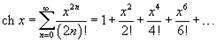 ; 5)
; 5) 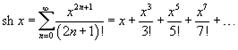 .
.
13)Задачи приводящие к понятию “двойного интеграла”.
Ответ: 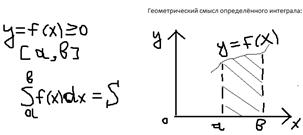
1)Объём цилиндрического тела: Пусть дано трёхмерное тело в пространстве – ограниченное снизу – плоскостью хОу, сверху: графиком функции z=f(x,y), и боковой цилиндрической поверхностью, с образующей параллельно оси OZ. 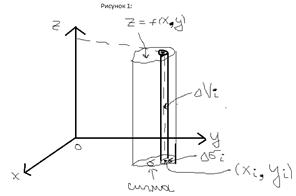
Основанием – является двумерная область 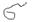 (сигма). Нужно найти – объём цилиндрического тела. Решение: Разобьём основание
(сигма). Нужно найти – объём цилиндрического тела. Решение: Разобьём основание  - на n участков;
- на n участков; 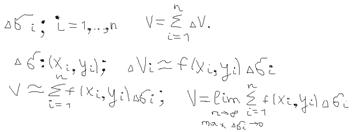 2)Масса неоднородной плоской пластины: Пусть мы имеем – плоскую пластинку, занимающую площадь
2)Масса неоднородной плоской пластины: Пусть мы имеем – плоскую пластинку, занимающую площадь 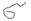 - плоскости xOy, на которой неравномерно распределена масса – с поверхностной плотностью
- плоскости xOy, на которой неравномерно распределена масса – с поверхностной плотностью  . Требуется найти: массу пластинки M.
. Требуется найти: массу пластинки M. 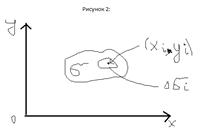 Разобьём
Разобьём 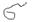 - на мелкие участки
- на мелкие участки 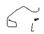 , так что их число – равно n. Тогда масса участка
, так что их число – равно n. Тогда масса участка  . Масса всей пластинки:
. Масса всей пластинки: 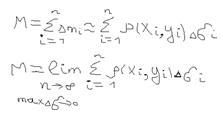
Дата добавления: 2015-01-19; просмотров: 267; Мы поможем в написании вашей работы!; Нарушение авторских прав |