Безынерционные нелинейные элементы

В теории и практике управления объекты управления рассматривают как преобразователи сигналов-носителей информации о цели функционирования объекта, его состоянии и воздействиях окружающей среды.

Если безынерционный элемент линейный, то он описывается полностью значением передаточного коэффициента.

Нелинейные зависимости между постоянными значениями входных и выходных сигналов

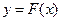(5.1)

задаются аналитически, графически или таблично.

В том случае, когда нелинейный элемент имеет один вход и один выход (рис. 5.2) особенно наглядны графики статических характеристик (рис. 5.3).

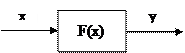
Рис. 5.2. Элемент системы как преобразователь сигналов

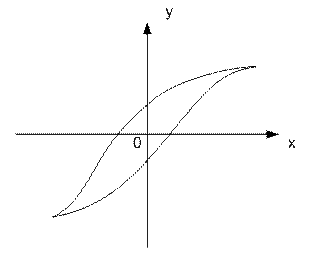
Рис. 5.3. Пример статической характеристики нелинейного элемента

Условия преобразования сигналов безынерционными нелинейными элементами зависят от уровней сигналов и не зависят от их частоты.

Примеры наиболее распространённых (типовых) нелинеаризуемых по методу малых отклонений нелинейных характеристик безынерционных элементов:

1. Двухпозиционное реле (звено с релейной характеристикой). Описать линейной зависимостью элемент с такой рабочей характеристикой невозможно, так как в рабочей точке имеется разрыв (рис. 5.4).

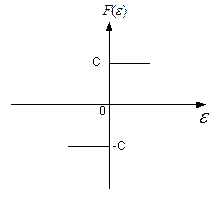Уравнение элемента:

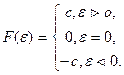(5.2)

Рис. 5.4. Статическая характеристика двухпозиционного реле

1. Трёхпозиционное реле (звено с релейной характеристикой и зоной нечувствительности) (рис. 5.5).

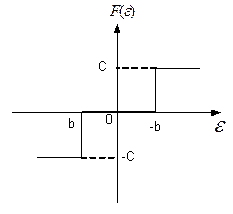Уравнение звена имеет вид

(5.3)

Рис. 5.5. Статическая характеристика

трехпозиционного реле

1. Ограничение (звено с характеристикой типа «насыщение») (рис. 5.6).

Необходимость исследования поведения системы «в большом» заставляет рассматривать характеристики элементов при больших значениях входных воздействий. В этом случае элемент может оказаться нелинейным, хотя и является линеаризуемым «в малом».

Уравнение элемента:

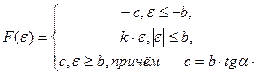(5.4)

Рис.5.6. Статическая характеристика типа «ограничение»

4. Зона нечувствительности (элемент с зоной нечувствительности) (рис. 5.7).

Уравнение элемента:

(5.5)

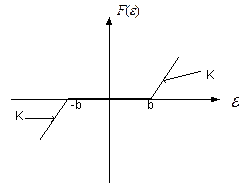
Рис.5.7. Статическая характеристика элемента с зоной нечувствительности

5. Ограничение с зоной нечувствительности (рис. 5.8).

Уравнение звена:

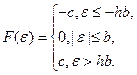(5.6)

Рис.5.8. Статическая характеристика элемен-

та с зоной нечувствительности и ог-

раничением

6. Двухпозиционное реле с зоной возврата (элемент с петлей гистерезиса) (рис. 5.9).

Уравнение элемента:

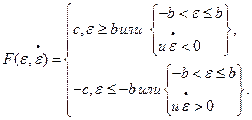(5.7)

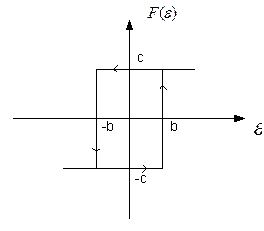
Рис.5.9. Статическая характеристика двухпозиционного реле с зоной возврата

7. Трехпозиционное реле с зоной нечувствительности и зоной возврата (элемент с зонами нечувствительности и неоднозначности) (рис. 5.10).

Уравнение элемента:

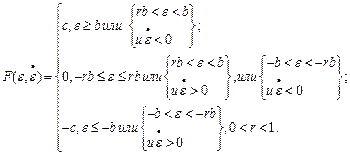(5.8)

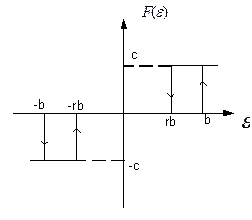
Рис.5.10. Статическая характеристика трёхпозиционного реле с зоной

нечувствительности и зоной возврата