
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнениями в форме Коши
Метод применяется для исследования устойчивости нелинейных систем по линеаризованным уравнениям для малых вариаций переменных.
Применим первый метод Ляпунова к дифференциальным уравнениям в пространстве состояний нелинейных систем.
Пусть динамическая система описывается уравнением
 (5.39)
(5.39)
где x - вектор состояния,  - вектор-функция.
- вектор-функция.
Обозначим через x*вектор координат исследуемого положения равновесия, т.е. решение системы уравнений  , и положим, что функция
, и положим, что функция  допускает разложение в ряд Тейлора в точке x*. Пренебрегая малыми высшего порядка по сравнению с малыми вариациями
допускает разложение в ряд Тейлора в точке x*. Пренебрегая малыми высшего порядка по сравнению с малыми вариациями  x, получим вместо уравнения (5.39) линеаризованную систему
x, получим вместо уравнения (5.39) линеаризованную систему
 , (5.40)
, (5.40)
где 
 -
-
- матрица первых производных нелинейной функции (матрица Якоби), вычисляемых в точке равновесия x=x* (рис.5.20).
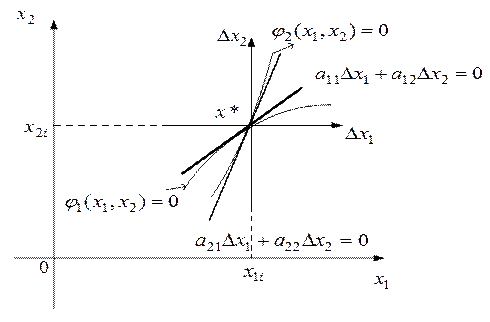
Рис.5.20. Линеаризация в окрестности положения равновесия
Согласно первому методу Ляпунова об устойчивости “в малом” положения равновесия нелинейной системы можно судить по результатам анализа линеаризованной системы:
· если все собственные значения матрицы А имеют отрицательные действительные части, т.е. линеаризованная система устойчива асимптотически, то положение равновесия устойчивое;
· если линеаризованная система неустойчива, то положение равновесия неустойчивое.
Первый метод Ляпунова имеет следующие недостатки:
· исследуется только устойчивость «в малом»;
· применим только для систем, линеаризуемых в окрестности положения равновесия.
Если требуется провести линеаризацию уравнения движения системы относительно опорной траектории 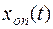 , являющейся решением уравнения
, являющейся решением уравнения
 (5.41)
(5.41)
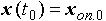 при некотором входном сигнале
при некотором входном сигнале  и начальных условиях ,
и начальных условиях ,
т.е. 
 (5.42)
(5.42)
то поведение x(t) нелинейной системы в окрестности опорной траектории может быть представлено с помощью отклонений (вариаций) 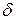 x(t) от опорной траектории:
x(t) от опорной траектории:  (5.43)
(5.43)
 Подставляя (5.43) в (5.41), имеем
Подставляя (5.43) в (5.41), имеем
 , (5.44)
, (5.44)
где  - вариация внешних воздействий,
- вариация внешних воздействий,
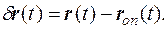
Разложим функцию F в ряд Тейлора в окрестности опорной траектории, ограничимся членами только первого порядка (линейными членами) и вычтем (5.42) из (5.44), получим, что вариации 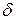 x(t) описываются системой линейных уравнений:
x(t) описываются системой линейных уравнений:
 , (5.45)
, (5.45)
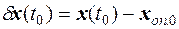 ,
,
где 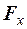 и
и  - матрицы частных производных вектор-функции F(t,x,r) по соответствующим аргументам,
- матрицы частных производных вектор-функции F(t,x,r) по соответствующим аргументам,
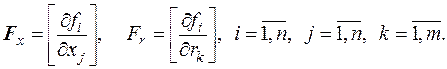
Дальнейший анализ нелинейной системы в окрестности опорного режима проводится методами анализа линейных систем, применяемыми к уравнениям в вариациях (5.45).
Дата добавления: 2015-01-29; просмотров: 216; Мы поможем в написании вашей работы!; Нарушение авторских прав |