Теорема Ляпунова (второй метод) о неустойчивости нелинейных систем.

Поскольку кроме области устойчивости нелинейная система может иметь целый ряд особых областей, то возникает потребность в отдельном определении области неустойчивости путем использования теоремы Ляпунова, которая дает достаточные условия неустойчивости систем.

Формулировка теоремы:

“Если при заданных в форме Коши уравнениях системы n-ого порядка производная 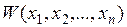от какой-нибудь функции Ляпунова 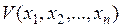окажется знакоопределенной, причем сама функция V в какой-нибудь области, примыкающей к началу координат, будет иметь знак, одинаковый со знаком производной W, то данная система неустойчива”.

Справедливость этой теоремы может быть проиллюстрирована так же, как и в предыдущем случае.

Второй метод Ляпунова универсален, так как не связан с линеаризацией уравнений движения и не накладывает особых ограничений на их правые части. Однако применение этого метода осложняется двумя причинами:

· достаточным характером утверждений, то есть если условия метода не выполнены, то об устойчивости положения равновесия ничего сказать нельзя, можно только порекомендовать подобрать другую функцию V(х);

· отсутствием общих рекомендаций по выбору функций Ляпунова.

Обычно функцию V(x) выбирают квадратичной формы

,

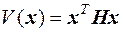(5.53)

где Н - положительно-определенная матрица. Это выражение для n=2 раскрывается так:

(5.54)

Для установления положительной определенности матрицы Н можно воспользоваться критерием Сильвестра, сводящимся к проверке положительности диагональных определителей матрицы. Например, для n=2 условия записываются так:

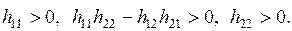(5.55)

Недостатком функции V(x) является то, что она не учитывает особенностей нелинейных систем.

Если статическая характеристика F( ) безынерционного нелинейного элемента в структурной схеме расчетного вида удовлетворяет следующим условиям:

· функция однозначна и непрерывна;

· F(0)=0;

· F( )>0, ≠ 0, т.е. график статической характеристики проходит через начало координат и располагается в первом и третьем квадрантах, то для этого практически важного случая А.И. Лурье и В.Н. Постников предложили следующую форму функции Ляпунова (квадратичная форма плюс интеграл от нелинейности):

(5.56)

Пример 5.7. Пусть линейная часть системы, приведенной к расчетному виду, имеет передаточную функцию

а нелинейный элемент удовлетворяет приведенным выше требованиям.

При отсутствии воздействия (r=0) положению равновесия системы соответствует x=0. Дифференциальное уравнение системы первого порядка в форме Коши запишется так (примем =x):

.

Выберем функцию Ляпунова в следующем виде

(5.57)

Продифференцируем эту функцию по времени в силу дифференциального уравнения системы:

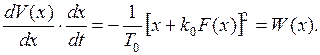
Получили отрицательно-определенную функцию W(x), что позволяет сделать вывод об асимптотической устойчивости положения равновесия.

Так как функция (5.57) определена для всех x и при имеем V(x) , положение равновесия асимптотически устойчиво в целом. Наконец, примем во внимание, что полученный результат справедлив для целого класса нелинейных функций F(x), удовлетворяющих введенным выше ограничениям, а это значит, что система абсолютно устойчива.

Пример 5.8.

В примере 5.3 заключение об устойчивости нелинейной системы по теоремам Ляпунова первого метода не принято. Воспользуемся вторым методом Ляпунова. Выберем скалярную функцию переменных состояния в виде квадратичной формы:

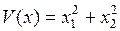
и продифференцируем по времени в силу дифференциальных уравнений системы:

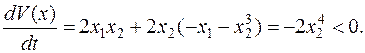
Получили отрицательно-определенную функцию, что означает асимптотическую устойчивость положения равновесия. Поскольку при 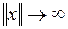имеем W(x) , положение равновесия устойчиво в целом.