
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критерий абсолютной устойчивости В.М. Попова
Рассматривается замкнутая система с одним нелинейным звеном.
Система называется асимптотически устойчивой, если при ненулевых ограниченных начальных условиях свободное движение y(t) ограничено при t є [0,∞) и lim y(t)=0 (t→∞).
Если окажется, что это свойство выполняется для любых нелинейных элементов из некоторого класса, то устойчивость называется абсолютной.
Теорема В.М. Попова.
Пусть выполняются условия:
1) все полюсы передаточной функции линейной части системы имеют отрицательные действительные части;
2) характеристика нелинейного элемента принадлежит сектору [0,k],
т.е. F(0)=0, 0 ≤ F(ε) / ε ≤ k при всех ε≠0 (рис.5.23);
3) существует действительное число q такое, что при всех ω є [0,∞)
выполняется неравенство
Re [(1+jωq)W(jω)]+1/k = u(ω)-qωυ(ω)+1/k >0,
q-произвольное действительное число.
Тогда при любых ограниченных начальных отклонениях от нулевого значения система будет абсолютно устойчивой.
| |
|
|

|
|




Алгоритм анализа абсолютной устойчивости:
1. Построим годограф модифицированной
частотной характеристики
W̃(jω) = Re W(jω) + jωImW(jω).
2. Находим параметр k (наименьший из возможных), удовлетворяющий условию п.2 теоремы.
3. Анализ геометрической интерпретации условий абсолютной устойчивости:
Рис.5.23. Характеристика
нелинейного элемента, принадле-
жащая сектору [0,k]
 3.1. Абсолютной устойчивости нет (рис.5.24).
3.1. Абсолютной устойчивости нет (рис.5.24).
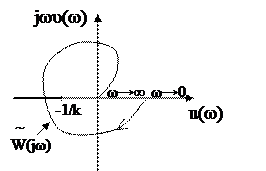
Рис.5.24. Годограф модифицированной частотной характеристики, когда абсолютной
устойчивости нет
3.2. Система абсолютно устойчива (рис.5.25).
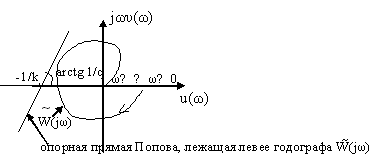
Рис.5.25. Годограф модифицированной частотной характеристики,
когда система абсолютно устойчива
3.3. Заключение об абсолютной устойчивости сделать не представляется возможным (рис.5.26).
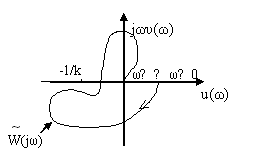
Рис.5.26. Годограф модифицированной частотной характеристики,
когда требуются дополнительные исследования для заключения
об абсолютной устойчивости
Приведем утверждение об абсолютной устойчивости часто встречающихся систем, в которых передаточная функция линейной части W(р) имеет один нулевой полюс, а нелинейный элемент F(  ) имеет зону нечувствительности:
) имеет зону нечувствительности:
“Пусть все полюсы передаточной функции W(р) линейной части системы лежат в левой полуплоскости (Rep<0), за исключением одного, равного нулю, причем  . Пусть, кроме того, характеристика F(
. Пусть, кроме того, характеристика F(  ) нелинейного элемента удовлетворяет условиям: F(
) нелинейного элемента удовлетворяет условиям: F(  )=0 при
)=0 при 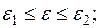 0<F(
0<F(  ) ≤ k(
) ≤ k(  -
- 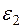 ) при
) при 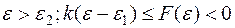 при
при 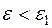 ; причем
; причем  ,
, 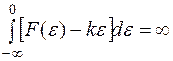 (т.е. график функции u=F(
(т.е. график функции u=F(  ) не приближается “плотно” к границе секторов, изображенных на рис. 5.27).
) не приближается “плотно” к границе секторов, изображенных на рис. 5.27).
Тогда, если существует такое действительное число q>0, что 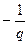 не является полюсом W(p), и для всех
не является полюсом W(p), и для всех 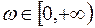 выполняется неравенство
выполняется неравенство
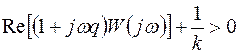 , (5.58) то при любых ограниченных начальных условиях процессы в системе останутся ограниченными и
, (5.58) то при любых ограниченных начальных условиях процессы в системе останутся ограниченными и  (t) при t
(t) при t  стремится к одной из точек отрезка покоя
стремится к одной из точек отрезка покоя 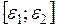 ”.
”.
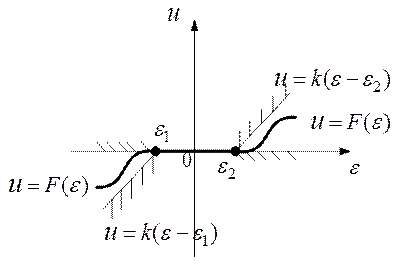
Рис.5.27.График функции u=F(  ) в границах секторов
) в границах секторов
Пример 5.9. Требуется исследовать абсолютную устойчивость системы, структурная схема которой (рис.5.28,а) включает релейный элемент с зоной нечувствительности (рис.5.28,в) или элемент с зонами нечувствительности, линейности и насыщения (рис.5.28,б).
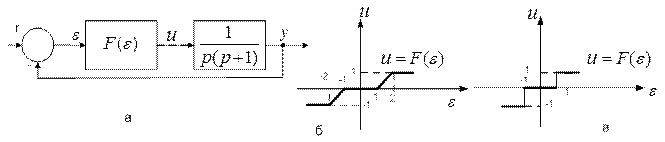
Рис.5.28.Структурная схема нелинейной системы и статические
характеристики нелинейного элемента
Передаточная функция 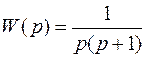 линейной части системы удовлетворяет условиям утверждения об абсолютной устойчивости, так как один полюс равен нулю (
линейной части системы удовлетворяет условиям утверждения об абсолютной устойчивости, так как один полюс равен нулю ( 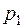 =0), а второй лежит в левой полуплоскости (
=0), а второй лежит в левой полуплоскости ( 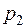 =-1), причем
=-1), причем  =1>0. Сравнивая характеристики нелинейных элементов с характеристикой изображенной на рис.5.27, определяем значения величин:
=1>0. Сравнивая характеристики нелинейных элементов с характеристикой изображенной на рис.5.27, определяем значения величин: 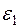 =-1,
=-1, 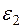 =1, k=1 для элемента рис.5.28, б и k=+
=1, k=1 для элемента рис.5.28, б и k=+ 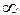 для элемента рис.5.28, в.
для элемента рис.5.28, в.
Запишем неравенство (5.58):
 .
.
Выделяя действительную часть, получаем
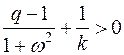 .
.
Очевидно, что при q>1 последнее неравенство выполняется при всех 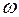 и любых k>0. Таким образом, точки отрезка покоя
и любых k>0. Таким образом, точки отрезка покоя 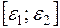 =[-1;1] являются устойчивыми положениями равновесия для системы (рис.5.28, а) с любым из рассматриваемых нелинейных элементов.
=[-1;1] являются устойчивыми положениями равновесия для системы (рис.5.28, а) с любым из рассматриваемых нелинейных элементов.
 5.10. Анализ устойчивости нелинейных систем по модели в форме
5.10. Анализ устойчивости нелинейных систем по модели в форме
Дата добавления: 2015-01-29; просмотров: 299; Мы поможем в написании вашей работы!; Нарушение авторских прав |