Эквивалентные статические характеристики систем с обратной связью.

Если два нелинейных элемента образуют контур с отрицательной обратной связью, то для получения эквивалентной статической характеристики необходимо исключить переменные и z в системе уравнений:

(5.21)

Отсюда выражение для выхода системы

(5.22)

Получена требуемая зависимость в неявной форме.

Пусть существует обратная нелинейность . Применим это преобразование к последнему выражению

(5.23)

т.е. получили статическую характеристику, обратную искомой,

отсюда

. (5.24)

Алгоритм графического построения требуемой статической характеристики системы (в предположении о её обратимости) следующий:

· строится обратная статическая характеристика ;

· характеристики и суммируются;

· определяется статическая характеристика, обратная суммарной:

.

а) б)

Рис. 5.15. Эквивалентные структурные схемы системы

Если существуют обратные нелинейности , то исходная структура преобразуема к эквивалентной, как показано на рис. 5.15.

Покажем справедливость этого преобразования.

Из выражения (5.23) находим

(5.25)

Пусть существует обратная нелинейность . Тогда, применив соответствующее преобразование к выражению (5.25), получим

(5.26)

Этому выражению соответствует соединение с обратной связью двух нелинейных элементов (рис. 5.15,б), эквивалентное исходному соединению (рис. 5.15,а) в смысле статической характеристики .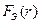

Сравнивая преобразованную структуру с исходной, замечаем, что нелинейные элементы поменялись местами, а их характеристики заменены на обратные. На практике такой прием иногда используется для упрощения реализации нелинейных элементов.

Эквивалентность структур, показанных на рис. 5.15 , имеет место и для динамических звеньев. В случае линейных звеньев с передаточными функциями и обратными будут операторы и соответственно.

Пример 5.1. Пусть нелинейный элемент типа «насыщение» со статической характеристикой охвачен отрицательной обратной связью в виде динамического звена с передаточной функцией (гибкая обратная связь)

(5.27)

Эквивалентное преобразование структуры показано на рис. 5.16.

а) б)

Рис. 5.16. Эквивалентные структуры системы с охватом нелинейного элемента

линейным динамическим звеном

В случае большого усиления нелинейного элемента в линейной зоне , когда , в схеме рис. 5.16,б можно игнорировать обратную связь с передаточным коэффициентом . В результате приближенно получим:

(5.28)

т.е. передаточную функцию пропорционально-интегрального звена.

Такой способ применим для реализации аналоговых регуляторов, реализующих ПИ-закон управления объектами.