Динамические нелинейные звенья САУ

В общем случае дифференциальные уравнения, описывающие элементы систем, являются нелинейными

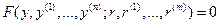. (5.9)

Иногда они разрешаются относительно старшей производной переменной выхода

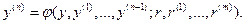(5.10)

Часто дифференциальные уравнения представляются в форме Коши:

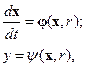(5.11)

где х – вектор переменных состояния; 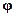-вектор-функция; - функция выхода. В уравнениях (5.9-5.11) предполагается, что нелинейные функции заданы аналитически.

Преобразование сигналов динамическими нелинейными элементами в значительной степени зависит как от уровней сигналов, так и от их частотных спектров.

Во многих случаях нелинейное динамическое звено представляется в форме линейной модели и дополнительного нелинейного элемента, учитывающего такие естественные факторы, как ограниченность управляющих воздействий, наличие зоны нечувствительности в измерительных и исполнительных элементах, люфтов в кинематических сочленениях или искусственное введение нелинейностей в алгоритмы управления для получения свойств, не достижимых в линейных системах.

Простейший пример такой модели – нелинейный интегратор

(5.12)

структурно изображается как последовательное соединение безынерционного нелинейного элемента и линейного интегрирующего звена (рис. 5.11).

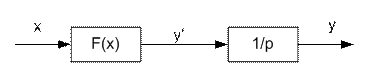
Рис. 5.11. Нелинейный интегратор

В этом примере нелинейные эффекты сосредоточены в безынерционном элементе, а динамические – в линейном элементе.