N-го порядка

Без потери общности рассмотрим процедуру линеаризации уравнения движения относительно опорной траектории на примере системы, описываемой дифференциальным уравнением второго порядка:

, (5.33)

где F- нелинейная функция своих аргументов.

Предположим, что задана опорная траектория , которая получается в результате решения уравнения (5.33) с начальными условиями и известным входным сигналом , т.е.

. (5.34)

Обозначим

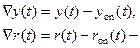(5.35)

отклонения от опорного режима,

где y(t) – решение уравнения (5.33) с начальными условиями и входным сигналом r(t). Графики функций приведены на рис. 5.18.

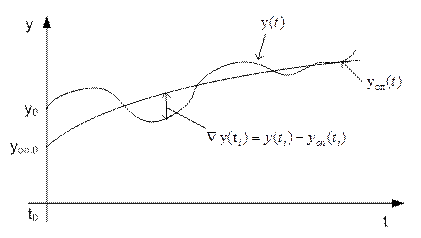
Рис. 5.18. Графики опорной траектории и реакции системы на входной

сигнал

Разложим функцию F в ряд Тейлора в окрестности опорной траектории, ограничиваясь членами только первого порядка (линейными членами):

, (5.36)

где индекс «оn» означает, что все частные производные рассчитываются на опорной траектории.

Первый член уравнения обращается в нуль, так как опорная траектория удовлетворяет уравнению (5.34).

Введем обозначения:

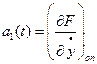, , , , . (5.37)

Тогда уравнение (5.36) переписывается в форме

(5.38)

с начальными условиями

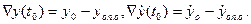
Его решение определяет отклонение от опорной траектории (см. рис. 5.18).

Пример 5.2. Пусть требуется провести линеаризацию системы, описываемой дифференциальным уравнением

с начальными условиями относительно опорной траектории .

Определим коэффициенты разложения функции F в ряд Тейлора:

,

.

Отсюда получим дифференциальное уравнение линеаризованной системы:

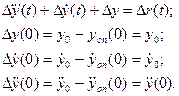
Структурная схема, соответствующая линеаризованному дифференциальному уравнению (знак условно опущен), приведена на рис. 5.19.

Рис. 5.19. Структурная схема САУ, соответствующая линеаризованному

дифференциальному уравнению

Алгоритм построения схемы:

1. Выражается член со старшей производной из дифференциального уравнения и представляется полученное соотношение с помощью сумматора, интегрирующих и усилительных звеньев;

2. Все низшие производные получаются как сигналы на соответствующих выходах последовательно соединенных интегрирующих звеньев;

3. Начальные условия представляются как постоянные во времени воздействия, приложенные на выходах интегрирующих звеньев.

Необходимое условие устойчивости Рауса (положительность всех коэффициентов характеристического уравнения системы

)

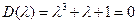не выполняется, так как . По критерию Гурвица должно выполняться неравенство условие Гурвица не выполнено, поэтому делаем вывод, что система неустойчива.

Корни характеристического полинома ,

- имеют положительную вещественную часть, поэтому согласно теоремам первого метода Ляпунова система неустойчива.