Пример 5. 3.

Проведем исследование устойчивости положения равновесия

системы с нелинейным демпфированием с помощью первого

метода Ляпунова.

Математическое описание системы в форме Коши имеет вид

Положение равновесия

Так как

то согласно (5.40) матрица

.

Линеаризация дает систему уравнений для малых отклонений, которую представим в векторно-матричной форме:

Собственные значения (характеристические числа) квадратной матрицы - корни уравнения

,

т.е. линеаризованная система находится на границе устойчивости. Согласно теоремам Ляпунова первого метода в этом критическом случае об устойчивости положения равновесия исходной нелинейной системы нельзя судить по линеаризованным уравнениям.

Теорема Ляпунова (второй метод) об устойчивости нелинейных

Систем

Формулировка теоремы:

“Если при заданных в форме Коши уравнениях системы n-го порядка можно подобрать такую знакоопределенную функцию Ляпунова 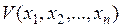, чтобы ее производная во времени 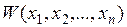тоже была знакоопределенной (или знакопостоянной), но имела знак, противоположный знаку V, то данная система устойчива”.

При знакоопределенной функции W будет иметь место асимптотическая устойчивость. Пусть заданы дифференциальные уравнения автоматической системы в форме системы уравнений первого порядка (форме Коши, уравнений состояния), полагая, что они записаны для переходного процесса в отклонениях всех переменных от их значений в установившемся процессе:

(5.46)

где функции произвольны и содержат любого вида нелинейности, но всегда удовлетворяющие условию

при

так как в установившемся состоянии все отклонения переменных и их производные равны нулю по самому определению понятия этих отклонений, и пусть имеется функция нескольких переменных (функция Ляпунова)

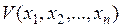, (5.47)

которая обращается в нуль в начале координат, т.е. при , и непрерывна в некоторой области вокруг него.

Функция V называется знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только начала координат.

Пример 5.4. Пусть и 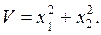Это будет знакоопределенная (положительная) функция, так как V=0 только тогда, когда одновременно и , и V > 0 при всех вещественных значениях и .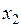

Функция - знакоопределенная отрицательная.

Функция V называется знакопостоянной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.

Пример 5.5. Функция при 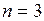- знакопостоянная (положительная) функция, так как она обращается в нуль при любом значении , если

Функция V называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.

Пример 5.6. Функция - знакопеременная, так как она положительна для всех точек плоскости справа от прямой и отрицательна слева от прямой (рис. 5.21).

Рис.5.21. Плоскость переменных ( )

Проиллюстрируем справедливость этой теоремы на примере системы третьего порядка ( 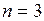). Возьмем знакоопределенную положительную функцию Ляпунова в виде

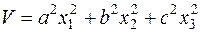, (5.48)

где a,b,c - произвольно заданные вещественные числа.

Будем придавать величине V возрастающие постоянные значения что означает

(5.49)

Первое из этих выражений соответствует одной точке (началу координат фазового пространства), а остальные - поверхностям эллипсоидов в фазовом пространстве, причём каждый последующий эллипсоид содержит внутри себя целиком предыдущий. Возьмем теперь производную от функции Ляпунова по времени:

(5.50)

и подставим сюда значения из заданных уравнений системы (5.46)

при n=3:

(5.51)

Если полученная таким путем функция 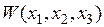окажется знакоопределенной отрицательной, т.е. если

(5.52)

во всех точках исследуемого фазового пространства, кроме одного только начала координат, где

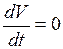при ,

то при любых начальных условиях изображающая точка М (рис.5.22), вследствие (5.52), будет двигаться в сторону уменьшения значений V , т.е. будет пересекать эллипсоиды извне внутрь.

Рис.5.22.Движение изображающей точки М относительно замкнутых

поверхностей, окружающих начало координат

В результате с течением времени изображающая точка М будет стремиться к началу координат фазового пространства (асимптотическая устойчивость) и уже никак не сможет выйти за пределы тех эллипсоидов, в которые она проникла. Это и означает затухание всех отклонений 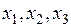в переходном процессе с течением времени, тем самым установлена устойчивость данной системы.

Теорема справедлива для исследования устойчивости систем управления не только при малых, но и при больших отклонениях, если для них имеют место исходные уравнения исследуемой системы управления.

Теорема Ляпунова обеспечивает получение достаточных условий устойчивости, которые не всегда будут и необходимыми, т.е. при выполнении условий теоремы система будет устойчива, но эти условия могут не охватить всей области устойчивости системы по параметрам, так как выбор функции V произволен и нет уверенности в том, что нельзя подобрать другой вариант функции V, который бы еще более полно охватывал область устойчивости данной системы.

Понятие устойчивости по Ляпунову допускает, чтобы при знакоопределенной функции V производная от нее W была не обязательно знакоопределенной или знакопостоянной, а могла быть и тождественно равна нулю во всем рассматриваемом фазовом пространстве. В этом случае изображающая точка М будет оставаться все время на какой-нибудь одной из поверхностей V=const, куда ее забросили начальные условия. В результате система хотя и не будет асимптотически приближаться к установившемуся состоянию, но все же будет все время в достаточной близости от него.

Если же функция W будет не знакоопределенной, а знакопостоянной, то траектория изображающей точки М не везде будет пересекать поверхности V=C, а может их касаться в тех точках, где W обращается в нуль (помимо начала координат). При решении задачи остается только проверить, не останется ли изображающая точка М там, где W=0.