структурной схемы

Если модель нелинейной системы представлена в форме структурной схемы, то можно записать систему дифференциальных уравнений в форме Коши или одно дифференциальное уравнение n-го порядка, тогда устойчивость исследуется по соответствующим схемам методов Ляпунова.

Однако устойчивость положения равновесия нелинейной системы можно исследовать и непосредственно по структурной схеме.

Пусть имеется модель в форме структурной схемы. Положим, что все нелинейные элементы безынерционные, тогда методика исследования устойчивости системы следующая:

1. Определяются равновесные режимы (если они существуют), устойчивость которых необходимо исследовать.

2. Производится расчет соответствующих этим состояниям значений переменных на входах всех нелинейных элементов системы.

Для определения значений переменных на входах нелинейных элементов можно применить аналитические, графические или численные методы. Анализ проводится по частной модели для равновесных режимов – динамические звенья заменяются безынерционными. Если звено интегрирующего типа (астатическое звено) с передаточной функцией:

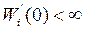, (5.59)

то в равновесном режиме переменная входа равняется нулю. Если в системе есть дифференцирующее звено

; , (5.60)

то в равновесном режиме его выход равен нулю.

3. Производим линеаризацию нелинейного элемента.

После того как найдено значение переменной на входе нелинейного элемента, заданного аналитически , линеаризация означает его замену безынерционным звеном

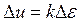(5.61)

с передаточным коэффициентом ,

равным значению производной в точке равновесия. Статическая характеристика нелинейного элемента в точке линеаризации должна быть гладкой (дифференцируемой).

Если статическая характеристика нелинейного элемента задана графически (рис. 5.29), линеаризация сводится к определению тангенса угла наклона касательной к статической характеристике в точке равновесия. Практически коэффициент усиления определяется как отношение приращений:

_.

Рис. 5.29. Линеаризация графически заданной статической характеристики

нелинейного звена

Если нелинейный элемент имеет несколько входов

,

то в результате линеаризации получим:

, (5.62)

где передаточные коэффициенты по различным входам равны значениям частных производных функции F в точке равновесия.

Например, линеаризация элемента перемножения двух переменных

(5.63)

в точке даёт . (5.64)

4. Составляется линейная модель системы.

В результате линеаризации всех нелинейных элементов для конкретного положения равновесия получается линейная модель для малых отклонений переменных на входах нелинейных элементов.

5. Исследование устойчивости нелинейной системы.

Анализ устойчивости системы «в малом» по линеаризованной модели в соответствии с первым методом Ляпунова даёт возможность судить об устойчивости выбранного положения равновесия нелинейной системы.

Анализ устойчивости системы «в большом» и «в целом» по нелинейной модели.

Пример 5.10. Проведём исследование устойчивости нелинейной системы, структурная схема которой изображена на рис. 5.30.

Рис. 5.30. Модель нелинейной системы

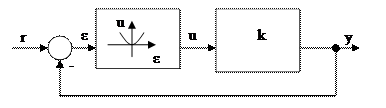Рис. 5.31. Модель системы для установившегося режима работы

По модели системы для установившегося режима работы (рис. 5.31) определим положения равновесия (равновесные режимы) этой системы. Если её параметры медленно изменяются, то положения равновесия также будут изменяться. В том случае, когда при некоторых значениях параметров рассматриваемое положение равновесия перестанет существовать, система будет вынуждена перескочить в другое устойчивое равновесное состояние, которое может быть весьма далёким от первоначального. Эволюция системы завершается скачкообразным изменением или, как говорят, катастрофой (например, разрушение экономики или строительного сооружения). В линейных системах положение равновесия единственно. Нелинейные системы могут иметь несколько положений равновесия. Можно ожидать, что при исследовании эволюций нелинейных систем окажется много вариантов возникновения устойчивых и неустойчивых положений равновесия.

Пусть нелинейный элемент системы расчётной структуры является квадратором:

. (5.65)

На вход системы подано постоянное воздействие , передаточный коэффициент линейной части равен k. Переменные системы определяются двумя параметрами – уровнем воздействия r и передаточным коэффициентом k, которые могут медленно изменяться.

Найдем значения переменной на входе нелинейного элемента в равновесных состояниях и изучим, как влияют на эти значения изменения параметров k и r.

Для решения задачи запишем уравнения статики:

. (5.66)

Рис. 5.32. Пример катастрофы типа «складка»

Графическое определение положений равновесия иллюстрирует рис. 5.32. В зависимости от соотношения параметров k и r система имеет два положения равновесия (прямая 1), одно (прямая 2) или ни одного (прямая 3). Соотношение параметров k и r, отвечающее касанию прямой и параболы, является критическим – сколь угодно малое изменение параметров приводит к качественному изменению ситуации. Множество значений (k,r), когда два положения равновесия сливаются в одно, называется множеством катастроф K.

Для аналитического определения множества K вместо системы (5.66) запишем одно уравнение для положения равновесия:

. (5.67)

Формула определения координат для положения равновесия

(5.68)

даёт действительное значение при условии

, ,

причём равенству отвечает критическая ситуация, когда два положения равновесия сливаются в одно. Множество катастроф К на плоскости (k,r) описывается уравнением

. (5.69)

Данный тип катастроф получил название «складка».

Если изменяется только один из параметров, например r, а k>0, то график зависимости положений равновесия имеет вид параболы (рис. 5.33). Ветви параболы при r>-k/4 соответствуют двум положениям равновесия. При r=-k/4 они сливаются в одно (точка катастрофы), а при дальнейшем уменьшении значения r положение равновесия исчезает.

Исследуемая система имеет два положения равновесия при уровнях постоянного воздействия r(t)>-0,25 и k=1.

Рис. 5.33. График зависимости положения равновесия от параметра

Значение r =- 0,25 соответствует катастрофе – малейшее уменьшение r(t) приводит к исчезновению положения равновесия, а малейшее увеличение – к появлению двух положений равновесия. Если r(t)>-0,25 ,то положениям равновесия отвечают следующие значения переменной на входе нелинейного элемента:

.

Графическая процедура определения координат точек равновесия, показанная на рис. 5.34, соответствует решению системы двух уравнений (5.66) при k=1 или уравнения

при r>-0,25. (5.70)

Рис. 5.34. Линеаризация нелинейного элемента

Линеаризуем статическую характеристику нелинейного элемента в этих точках; получим

.

Характеристические полиномы замкнутых линеаризованных систем имеют вид

.(5.71)

Один из полиномов этого выражения не удовлетворяет необходимому условию устойчивости Рауса (знак «минус» при свободном члене). Для устойчивости системы с другим полиномом в соответствии с критерием Гурвица необходимо и достаточно выполнение условия

, т.е. r<20 .

Таким образом, делаем вывод о том, что из двух положений равновесия, в которых может находиться система при постоянном значении воздействия r>-0,25 , устойчивым является одно

и только при ограничении сверху уровня воздействия r(t)<20. При рассчитанных ограничениях входного воздействия нелинейная система устойчива «в малом» и «в большом».